LeetCode

LeetCode-方法论-Floyd's Algorithm

这篇笔记记录Floyd算法，及若干与之相关的Leetcode问题。体会本题是怎样将问题转化的。当原问题棘手时，找到合适的方向可以转化为简单问题。

#141 Linked List Cycle

  • 描述

    1
    2
    3
    Input: head = [3,2,0,-4], pos = 1
    Output: true
    Explanation: There is a cycle in the linked list, where tail connects to the second node.

  • 思路

    如果存在环，兔子与乌龟会第二次相遇；否则除了起点，龟兔不会再相遇。

  • 实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    bool hasCycle(ListNode* head){
        if(!head) return false;
        ListNode* rabbit=head;
        ListNode* turtle=head;


        while(rabbit && turtle){
            rabbit = rabbit->next;
            turtle = turtle->next;
            
            if (rabbit) rabbit=rabbit->next; // one step faster than the turtle
            if (rabbit && (rabbit==turtle))
                return true;
        }
        return false;
    }

#287 Find the Duplicate Number

  • 描述

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    Input: [3,1,3,4,2]
    Output: 3
    Note:

        You must not modify the array (assume the array is read only).
        You must use only constant, O(1) extra space.
        Your runtime complexity should be less than O(n2).
        There is only one duplicate number in the array, but it could be repeated more than once.

    依照本题意，数组中一定有重复元素，找到数组中重复出现的元素。

  • 思路

    就题意而言，数组元素唯一和数组元素有重复的区别可用下图表示：

    1) 当给定数组中无重复元素时，如nums={3,4,5,2,1}。以第一行为当前位置，第二行为下一位置。小人从位置0开始走最终走到5停止。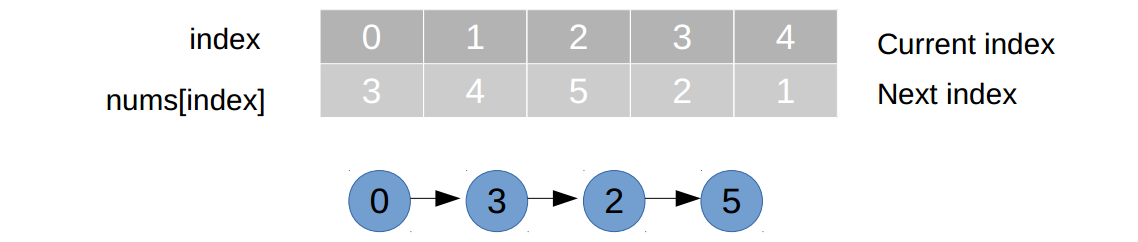

    路经无环

    2) 当给定数组中有重复元素时，如nums={1，4，6，5，6，2，3}。小人从位置0开始走，路经有环始终不会停止。而且被两个箭头指向的节点6为重复元素。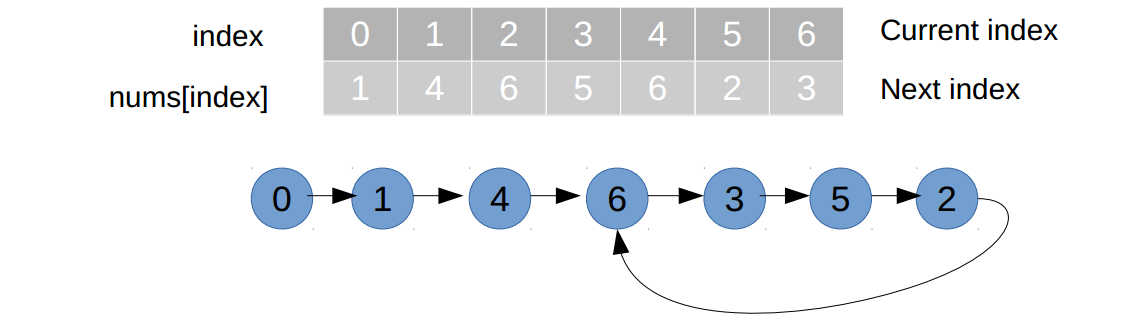

    路经有环

  • 实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    int findDuplicate(vector<int>& nums) {
        int turtle = nums[0];
        int rabbit = nums[0];
        do{
            turtle = nums[turtle];      // one step
            rabbit = nums[nums[rabbit]]; // two steps
        }while(turtle != rabbit);  
        
        int ptr1 = nums[0];
        int ptr2 = turtle;
        while(ptr1 != ptr2){
            ptr1 = nums[ptr1];
            ptr2 = nums[ptr2];
        }
        return ptr1;              
    }

    当龟兔位于同起点，向相同的方向跑，如果赛道无环，乌龟永远追不上兔子。若赛道有环，兔子会再次追上乌龟。这就是Floy’s 算法的来源。

    表面上与龟兔赛跑无关，在逻辑上构建出类似链表后，就水到渠成了。

    本题并不复杂，但当经过转化后时间空间复杂度达到若干方法中较优。时刻有转化问题的意识。

关键：问题转化，龟兔赛跑