Machine Learning

模型评价-混淆矩阵(Confusion Matrix)

这篇笔记记录Confusion Matrix。

当训练好了模型，需要评价它的性能。错误率和准确率是常用的，一般为了测试一个模型的正确性，用这个指标，尤其对于极度均衡的数据。但是对于极度偏斜的数据，用准确率评价模型很可能得到的结果表示，这个模型还不如随机猜测的准确率高。此时准确率不足以衡量模型性能。所以必要使用其他性能指标。

由混淆矩阵得到的Precision， Recall 和 F1度量，F-beta度量。

其定义不赘述，看下图。

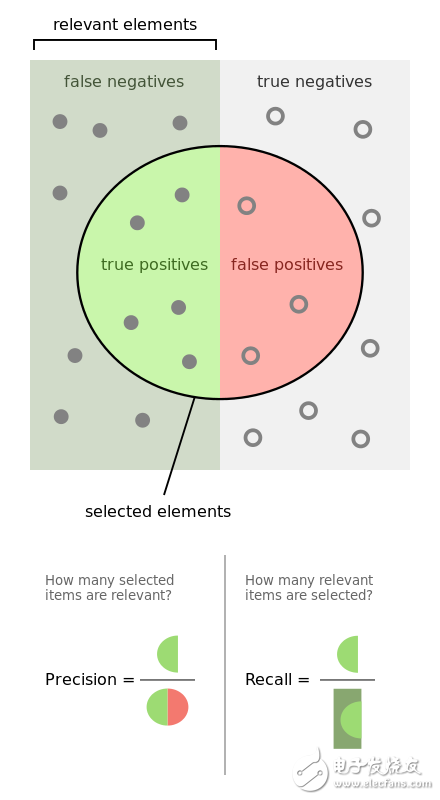
图中，P，R的含义在清楚不过了。

使用真实数据集算一下。

引入数据，把它变为极度偏斜的二分类问题：

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
x = digits.data
y = digits.target.copy()

y[digits.target == 9] = 1
y[digits.target != 9] = 0

# 分训练样本和测试样本
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=666)

这里使用Logistic Regression对其学习：

1
2
3
4
5
6
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(x_train, y_train)
acc = log_reg.score(x_test, y_test)
y_log_predict = log_reg.predict(x_test)
print(acc)

得结果：0.975555555556。注意数据集是很不平衡的，所以这个值不可靠。

根据混淆矩阵的定义，可得：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def TN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict == 0))


def TP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict == 1))


def FN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict == 0))


def FP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict == 1))


def confusion_matrix(y_true, y_predict):
    return np.array([[TN(y_true, y_predict), FP(y_true, y_predict)],
                     [FN(y_true, y_predict), TP(y_true, y_predict)]])

# 打印出混淆矩阵：
print(confusion_matrix(y_test, y_log_predict))

结果：

1
2
[[403   2]
 [  9  36]]

一般来说，最优情况是，其对角线的值最大，斜对角线值为0。详见多分类问题的混淆矩阵。

Precision=0.947368421053， Recall=0.8。标准是，此而值同时越大模型性能约优。可以说这个模型的性能还不错。

敲黑板啥是R，“所有实际为正的样本，我的模型有多少也认为为正”。啥是P，“所有我的模型认为为正的样本，有多少确实为正”。可以体会到，P&R 是不同角度的两个指标。根据信息论观点，引入相似但不相同的信息有助于减少系统的不确定性。两个指标同时考虑比单单考虑一个指标更能确定模型的性能。实际上，可能的情况下，对于一个训练好的模型，所有可能的指标都应该看看。
另一方面，P&R两者的关注点不同，所以对于不同的实际任务，P&R值的相对大小可以有所不同。举例，对于病例数据，尽可能希望所有实际有病的样本，模型也认为有病。即实际有病的样本模型都可以判断出来，即使没病的模型认为有病，没关系，复查就好了。这就是R值越大模型性能越好。反而P值相对不重要。