Machine Learning

模型评价-PR曲线

Precision和Recall是两个矛盾的度量，一个变大时，另一个就变小。怎样格式化P-R的关系呢。P-R曲线。

绘制P-R曲线

根据每一个样本得到不同的分类平面，即许多个不同的模型。对每一个模型计算P&R值，最后以P，R为横纵轴绘图。

1. 如何得到不同模型

图示

假设已经使用训练样本训练出一个Logistic Regression模型log_reg，测试集x_test，y_test。调用训练好模型的decision_function()，返回所有分类平面。其实Logistic Regression的默认分类平面是y=0，即threshold=0。

decision_scores记录所有分类平面：

1
2
3
4
decision_scores = log_reg.decision_function(x_test)  
print(len(decision_scores))         #  450
print(np.min(decision_scores))      #  -85.6861241675
print(np.max(decision_scores))      #  19.8896068857

当threshold = 0时，即默认分类平面对应的模型各指标：

1
2
3
4
5
y_predict = log_reg.predict(x_test)            
print(confusion_matrix(y_test, y_predict))    #  [[403   2]
                                              #   [  9  36]]
print(precision_score(y_test, y_predict))     #  0.947368421053
print(recall_score(y_test, y_predict))        #  0.8

当使用threshold = -5为分类平面时，三指标：

1
2
3
4
5
6
# 移动threshold到-5得到不同的模型：
y_predict_m5 = np.asarray(decision_scores >= -5, dtype='int')
print(confusion_matrix(y_test, y_predict_m5))   #  [[390  15]
                                                #   [  5  40]]
print(precision_score(y_test, y_predict_m5))    #  0.727272727273
print(recall_score(y_test, y_predict_m5))       #  0.888888888889

相较threshold = 0的模型，P下降，R上升。

当使用threshold = 5为分类平面时，三指标：

1
2
3
4
5
6
# 移动threshold到5得到不同的模型：
y_predict_5 = np.asarray(decision_scores >= 5, dtype='int')
print(confusion_matrix(y_test, y_predict_5))    #  [[404   1]
                                                #   [ 21  24]]
print(precision_score(y_test, y_predict_5))     #  0.96
print(recall_score(y_test, y_predict_5))        #  0.533333333333

相较threshold = 0的模型，P上升，R下降。

2. 绘制曲线

得到每一个threshold对应的P，R值，绘制P-R曲线。

有了对某一个threshold的理解，现在相隔0.1取一个threshold，获得所有P，所有R：

1
2
3
4
5
6
7
8
9
10
11
import matplotlib.pyplot as plt
precisions = []                           # 记录所有P
recalls = []                              # 记录所有R
# 相隔0.1取一个threshold值保存：
thresholds = np.arange(np.min(decision_scores), np.max(decision_scores), 0.1)

# 记录每一个threshold对应模型的P&R:
for threshold in thresholds:
    y_predict = np.array(decision_scores >= threshold, dtype='int')
    precisions.append(precision_score(y_test, y_predict))
    recalls.append(recall_score(y_test, y_predict))

绘图thresholds vs precisions和thresholds vs recalls：

1
2
3
4
5
6
plt.plot(thresholds, precisions, label='P')
plt.plot(thresholds, recalls, label='R', )
plt.legend(loc='center left', prop={'size': 10})
plt.xlabel('threshold')
plt.ylabel('P/R')
plt.show()

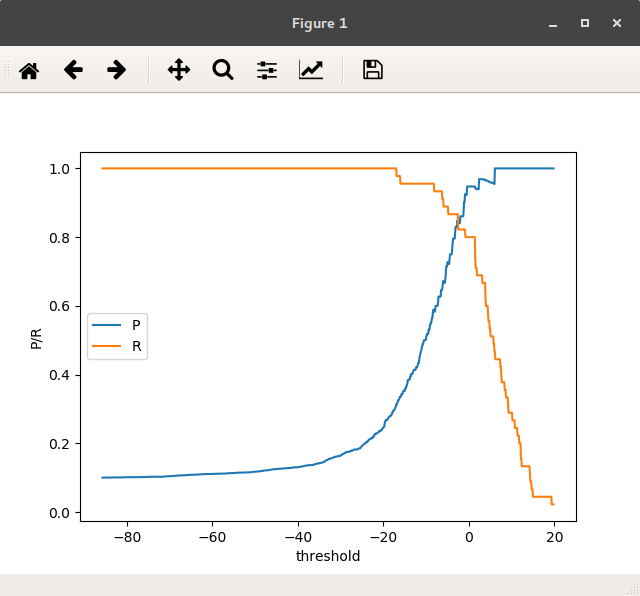
结果：

图 不同threshold的P/R值

绘制precision vs recall：

1
2
3
4
5
plt.plot(precisions, recalls, label='P-R')
plt.legend(loc='lower left', prop={'size': 10})
plt.xlabel('P')
plt.ylabel('R')
plt.show()

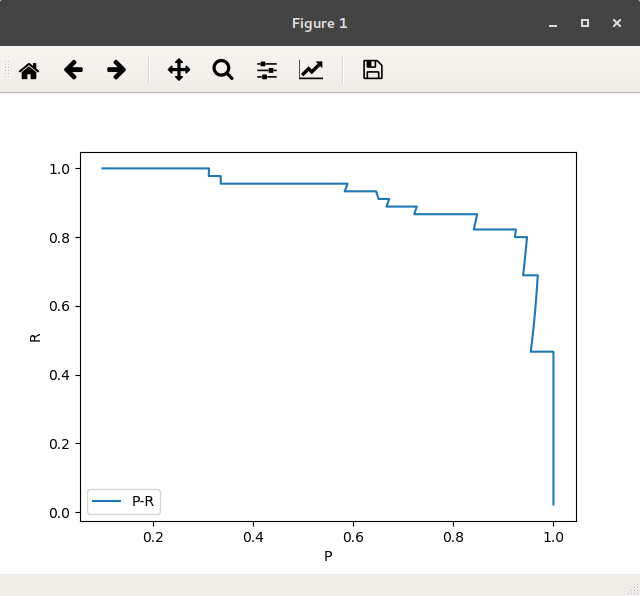
结果：

图 P/R曲线

敲黑板经过实验得出：

  1. 最优threshold基本都在0附近，因此可以说，若没有对某一指标有具体的定量要求，只用判别threshold=0时的指标就可以对整个模型的性能进行评估了。
  2. 第二点，一个二分类模型尝试移动分类平面，可以得到对于P&R不同重视程度的模型。

对于P-R曲线的几点补充：

  • 实际中，对P-R曲线进行平滑操作
  • 如果由若干个模型的P-R曲线在同一个图中，如何判断哪个最优。
    1. 看哪一个曲线把其他的“包住”
    2. 比较每条曲线与坐标轴围成的面积

附件

sklearn package中的绘制P-R曲线的方法：

1
2
3
4
5
6
7
8
9
10
from sklearn.metrics import precision_recall_curve

pres, recs, thrs = precision_recall_curve(y_test, decision_scores)

plt.plot(thrs, pres[:-1], label='thr-P')
plt.plot(thrs, recs[:-1], label='thr-R', )
plt.legend(loc='center left', prop={'size': 10})
plt.xlabel('threshold')
plt.ylabel('P/R')
plt.show()

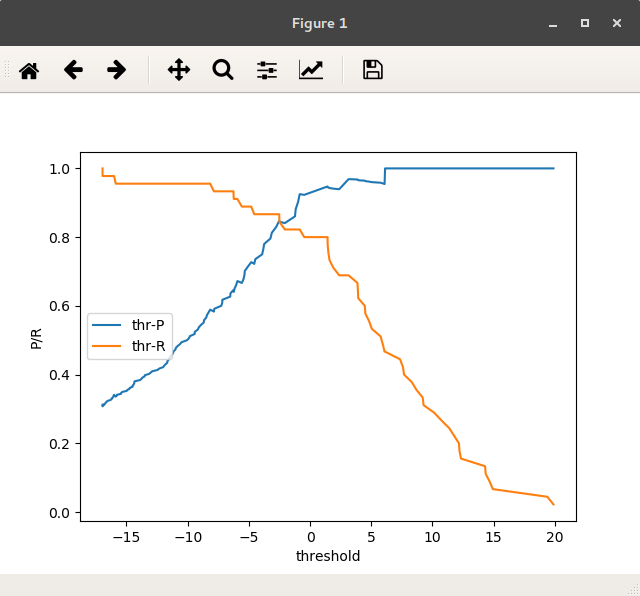
不同threshold的P/R值:

图 不同threshold的P/R值 built-in方法

与上述实现不同在于，上述实现的threashold值从decision_scores的最小值到最大值，而package中函数把threshold值小于-18的值忽略未记，因为图一中这部分对于用户是没有决策贡献的。抓住要矛盾。

1
2
3
4
5
plt.plot(pres, recs, label='P-R')
plt.legend(loc='lower left', prop={'size': 10})
plt.xlabel('P')
plt.ylabel('R')
plt.show()

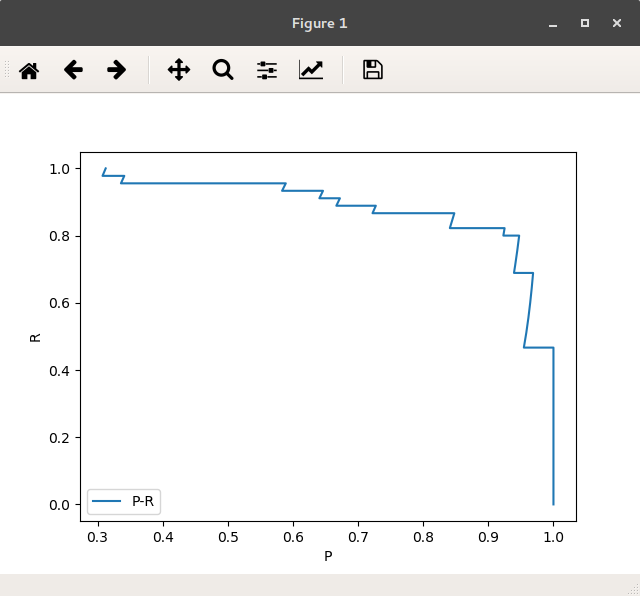
P/R曲线

图 P/R曲线 built-in方法