226,112,589
写在前面:
- 别忘了递归终止条件。
- 明确递归函数的定义,并确保实现中函数保持定义不变。
- 理解问题。分析出递归结构。
- 大脑不适应递归,像盗梦空间,你需要跳进跳出。一层一层跳入,到底,再一层一层跳出。令人恍惚的是每一层的变量都长一样!
- 用彩色笔画递归树,不同颜色表示不同层,你就不懵了。
- 除了多见类似的问题,训练大脑。目前找不出其他方法让大脑适应递归。
- 深度优先遍历,回朔,都是递归。
- 递归函数占用额外空间,调用递归函数需要额外开销。
- 由于二叉树天然具有递归性,解决问题时可以从树中拿出一个合适大小的子树,来构建出初步代码。
- 大多问题与二叉树的4种常见的遍历方法有关。
- 一个模式:移动控制+结点操作
#226 Invert Binary Tree
描述:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15Input:
4
/ \
2 7
/ \ / \
1 3 6 9
Output:
4
/ \
7 2
/ \ / \
9 6 3 1思路
递归树:
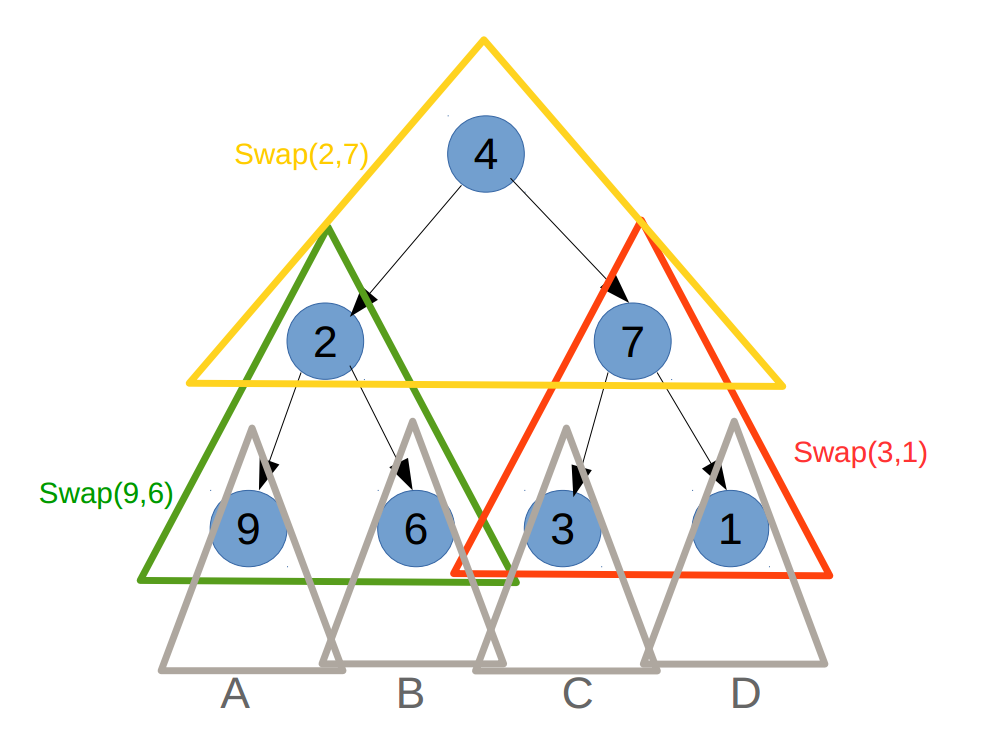
要想实现问题描述的Invert,就需要从下往上Swap。具体说:
先执行灰三角A,swap(空,空);执行灰三角B,swap(空,空);执行绿三角,swap(9子树, 6子树);
先执行灰三角C,swap(空,空);执行灰三角D,swap(空,空);执行红三角,swap(3子树, 1子树);
最后执行黄三角,swap(2子树, 7子树)
结束。
代码实现:
1
2
3
4
5
6
7
8
9
10
11// 定义:交换以root为跟的左右子树,返回交换后的root。
TreeNode* invertTree(TreeNode* root){
if (!root)
return NULL;
invertTree(root->left);
invertTree(root->right);
swap(root->left, root->right);
return root;
}这个过程其实是Binary Tree的后续遍历:
1
2
3
4
5
6
7
8
9
10
11// 定义:打印输出root的值。
void postOrder(TreeNode* root){
if (!root)
return NULL;
postOrder(root->left);
postOrder(root->right);
cout<<root->val<<endl;
return;
}除了返回值,唯一的不同是前者执行交换root的左右子树,后者执行打印root->val。本质一样:后续遍历。
相似问题:#337 #508
#112 Path Sum
描述:
1
2
3
4
5
6
7
8
9
Given the below binary tree and sum = 26,
5
/ \
4 8
/ / \
11 13 4
return true,
as there exist a root-to-leaf path 5->8->13 which sum is 26.
思路
两种思路,先序遍历,保存所有root-to-leaf的路径值,后搜索。见这里,效率低。
另一种思路,递归树:
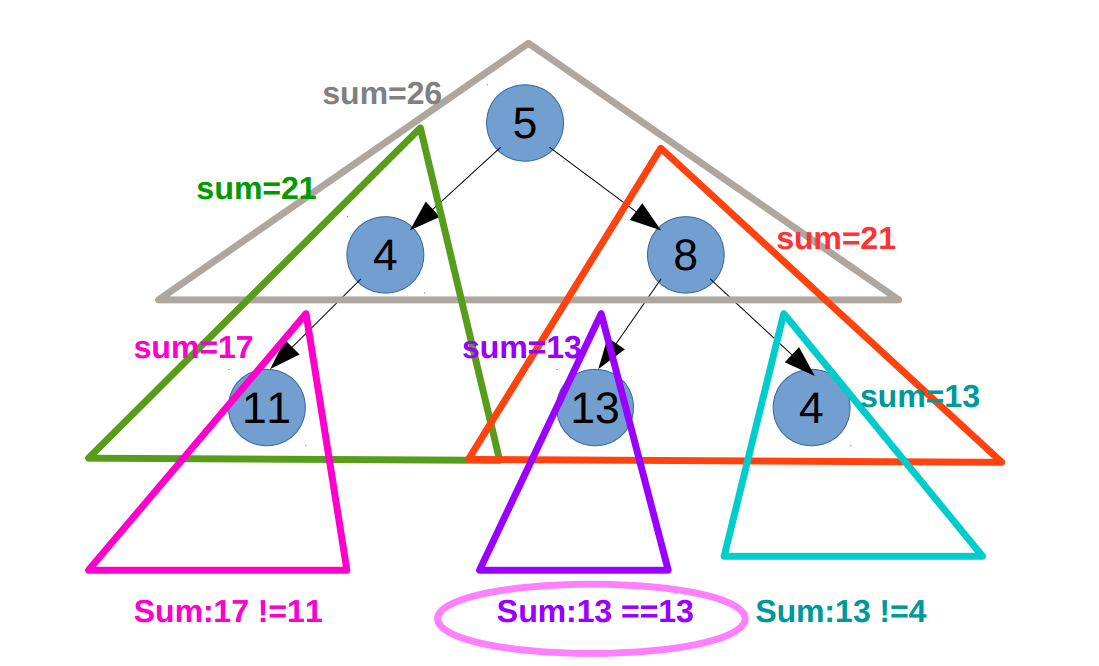
执行过程,即是先序遍历,每“跳进”一个新的子树,就更新sum值。最终可以找到
sum:13==13,实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21// 定义: 以root为根的树中是否含有和为sum的路径
bool hasPathSum(TreeNode* root, int sum) {
// if root is NULL
if (!root)
return false;
// if this root is a leaf
if (root->left == nullptr &&
root->right == nullptr)
return root->val == sum;
// if root has the left child
if (hasPathSum(root->left, sum-root->val))
return true;
// if root has the right child
if (hasPathSum(root->right, sum-root->val))
return true;
return false;
}本质上还是先序遍历。敲黑板sum值在“跳进”后,变小,“跳出”后,又变回原来值。“跳进”表示,递归调用自己,“跳出”表示,这次递归调用执行到return语句。就本问题而言,但遍历到结点13时,满足
sum 13==13,所以在此返回true。遍历不再执行,所以右下角结点4从未被遍历到。
#589 N-ary Tree Preorder Traversal
描述
1
Given an n-ary tree, return the preorder traversal of its nodes' values.
逻辑
多叉树的先序遍历,思路很直接:先遍历root,后对于这个root的所有子节点,以子节点为新的root做同样的操作。
这里的操作具体说是将节点值放入vector。实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28void travel(Node* root, vector<int>& res){
if (!root)
return;
res.push_back(root->val); // root
for (Node* chld : root->children) // all children of root
travel(chld, res);
}
vector<int> preorder(Node* root){
vector<int> res;
travel(root, res);
return res;
}
// The definition of Node
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
敲黑板这里有个模式:对于几乎所有树的问题,本质上都是树的遍历。遍历本质上是结点的移动控制。而对于当前节点来说,它的value是可得到的,对这个value的操作称之为结点操作。