LeetCode

LeetCode-方法论-DP-一

总结一下与DP相关的问题。

64, 300(LIS), LCS, 120, 62, 303, 198,

DP特点：

  • 把重复计算的结果保存下来，避免重复计算（记忆机制）。
  • DP自下而上执行，通过可计算的最小子结构逐步向上求值，直到得到最终值。
  • 通常问题是要求最优值。

实现DP方法：

  • 画递归树，自顶向下思考，自下而上实现
  • 找到合适的状态及状态转移方程
    • 状态：递归树的结点啥定义，即每一步记忆的内容是啥memo[i]，即函数是啥。
    • 状态转移方程：结点怎样实现，即怎样得到memo[i]，即函数怎么做。

#64 Minimum Sum Path

问题描述：

1
2
3
4
5
6
7
8
9
10
11
12
Given a m x n grid filled with non-negative numbers, find a path from **top left** to **bottom right** which minimizes the sum of all numbers along its path.
Note: You can only move either *down* or *right* at any point in time.

Input:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]

Output: 7
the path 1→3→1→1→1 minimizes the sum, which is 7.

  • 思路

    记忆的逐步实现：

    • 初始化：memo所有元素初始化为0，且第一行第一列特殊处理。

    • 状态定义：memo[i][j]表示从左上角到Input[i][j]的最短路径。

    • 状态转移方程：memo[i][j] = Input[i][j] + min(memo[i][j-1], memo[i-1][j])。

    • 返回值：memo[i-1][j-1]

      图示：

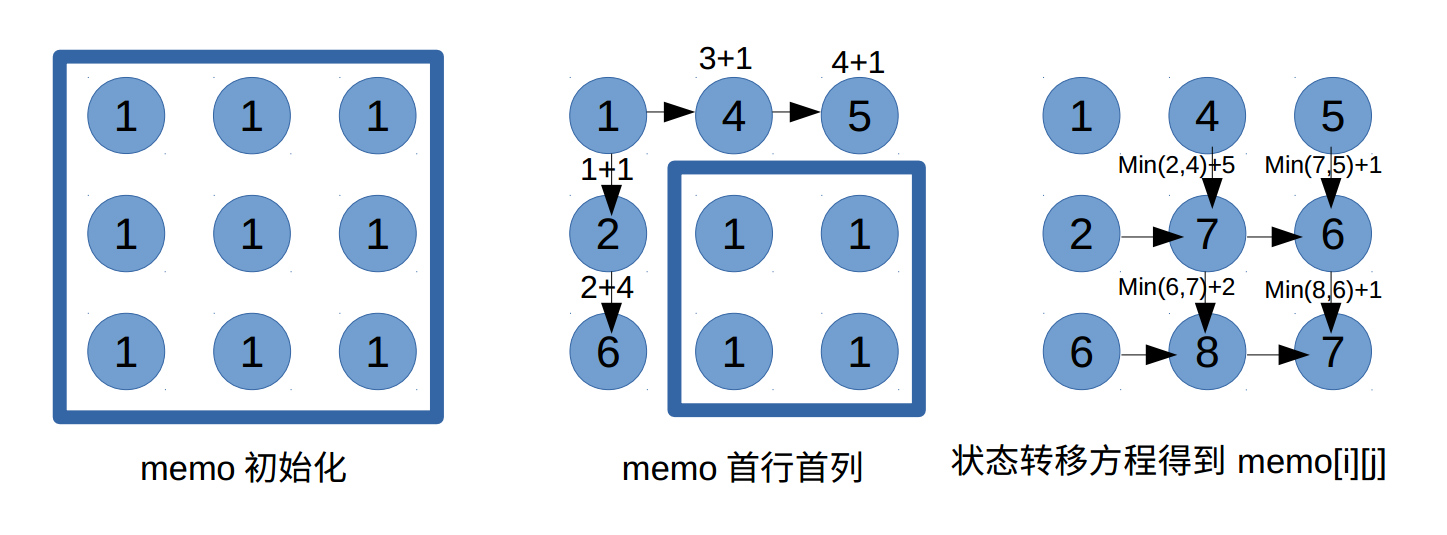
      最终返回memo右下角值：7。

  • 看图说话

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();

        for (int i=1; i<m; i++)
            grid[i][0] += grid[i-1][0];

        for (int i=1; i<n; i++)
            grid[0][i] += grid[0][i-1];

        for (int i=1; i<m; i++){
            for (int j=1; j<n; j++)
                grid[i][j] += min(grid[i][j-1], grid[i-1][j]);
        }

        return grid[m-1][n-1];
    }

#300 Longest Increasing Subsequence

  • 描述
1
2
3
4
5
Input: [10,9,2,5,3,7,101,18]
Output: 4 
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4. 

返回最长公共子序列的长度。

  • 逻辑

    • 初始化：mem数组为全1。
    • 状态的定义：定义mem[i]为以nums[i] 为结尾的最长上升子序列的长度。
    • 状态转移方程：当前元素nums[i]与其前元素逐个比较，如果当前元素大于其前某个元素nums[j]，更新mem[i]=max(mem[i], 1+mem[j]).
    • 最终：找到mem数组中最大的值即可。DONE

  • 实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    int lengthOfLIS(vector<int>& nums) {
        if (nums.size() == 0)
            return 0;

        // calculate memo
        vector<int> memo(nums.size(), 1);
        for (int i=1; i<nums.size(); i++){
            for (int j=0; j<i; j++){
                if (nums[i]>nums[j])
                    memo[i] = max(memo[i], 1+memo[j]);
            }
        }

        // get max length
        int res = memo[0];
        for (int i=0; i<memo.size(); i++)
            res = max(res, memo[i]);

        return res;
    }

关键：由最小已知求未知，接着根据当前的已知求进一步的未知， 状态的定义，找到状态转移方程，

#LCS Longest Common Subsequence

  • 描述
1
给定两个字符数组，求其公共的子序列。公共子序列的元素在原序列中可以不连续。
  • 逻辑
  • 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
string getLCS(const string& s1, const string& s2){
		int m = s1.size();
		int n = s2.size();
		
		vector<vector<int>> memo(m ,vector<int>(n, 0));
		// initilize memo
		for (int i=0; i<m; i++){
			if (s1[i]==s2[0]){
				for (int k=i; k<m; k++)
					memo[k][0] = 1;
				break;
			}	
		}

		for (int j=0; j<n; j++){
			if (s2[j]==s1[0]){
				for (int k=j; k<n; k++)
					memo[0][k]=1;
				break;
			}	
		}

		// DP progress for the rest
		for (int i=1; i<m; i++){
			for (int j=1; j<n; j++){
				if (s1[i]==s2[j])
					memo[i][j] = 1 + memo[i-1][j-1];
				else
					memo[i][j] = max(memo[i-1][j], memo[i][j-1]);
			}	
		}

		cout<<"The lenght of the LCS: "<<memo[m-1][n-1]<<endl;
		// get the longest common sequence
		string res = "";
		while (m>=0 && n>=0){
			if (s1[m] == s2[n]){
				res = s1[m] + res;
				m--;
				n--;
			}
			else if (m==0) n--;
			else if (n==0) m--;
			else{
				if (memo[m-1][n]>memo[m][n-1]) m--;
				else n--;
			}
		}
		return res;
	}

#120 Triangle

  • 描述
1
2
3
4
5
6
7
8
9
10
11
12
13
Given a triangle, find the minimum path sum from top to bottom. 
Each step you may move to adjacent numbers on the row below.

For example, given the following triangle

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).

  • 逻辑

    bottom-up DP或者Top-down DP。使用Top-down：

    • 状态定义：triangle[i][j] 表示从顶端到第i行第j个位置的最小路径

    • 状态转移方程：见下图

      Top-down DP过程如下图表示：其中椭圆结点构成的triangle为源triangle，矩形结点构成的triangle就是DP的mem，即状态。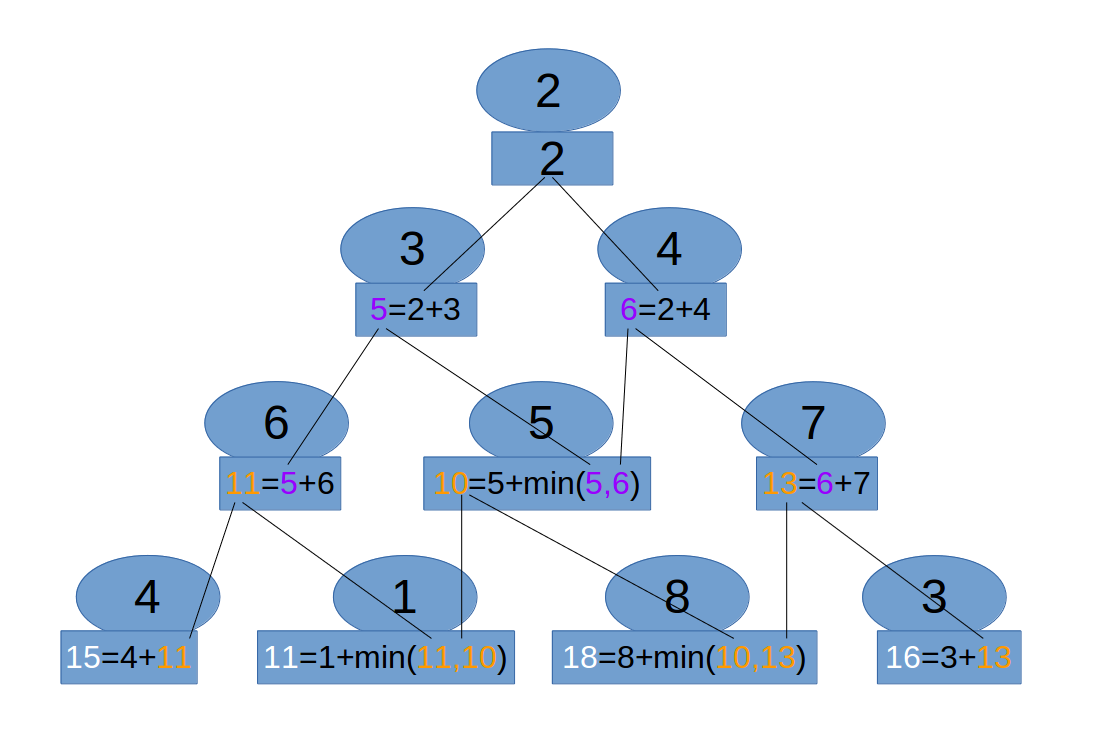

  • 看图说话

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    int minimumTotal(vector<vector<int>>& triangle) {
        int n = triangle.size();  // height of this triangle

        triangle[0][0] = triangle[0][0];  

        for (int i = 1; i<n; i++){    // 
            // 这一行第一个值
            triangle[i][0] += triangle[i-1][0];  
            // 这一行最后一个值
            triangle[i][i] += triangle[i-1][i-1];
            // 这一行其他值
            for (int j=1;j<i;j++)
                triangle[i][j] += min(triangle[i-1][j-1], triangle[i-1][j]);
        }
        // 源triangle被修改了，所以最终结果在这个triangle的最后一层找最小值即可
        return *min_element(triangle[n-1].begin(), triangle[n-1].end());

    }

关键：当处理最值相关问题，考虑DP

#62 Unique Path

  • 描述
1
从grid的左上角位置到右下角位置有几种走法？只能向下走或向右走。

  • 逻辑

    Top-down DP或者Bottom-up DP，使用Bottom-up：

    • 状态定义：从(i,j)出发到终点(m-1,n-1)由多少条路径。
    • 状态转移方程：同Fibonacci()，numPath(i,j) = numPath(i,j+1) + numPath(i+1,j);
    • 初始化最右边和最下边值为1. 过程从这里开始up。

  • 实现

    • Bottom-up
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      int uniquePaths(int m, int n) {
          vector<vector<int>> memo(m, vector<int>(n, -1));
          // 初始化最下行
          for (int i=0;i<m; i++)
              memo[i][n-1] = 1;
          // 初始化最右行
          for (int j=0; j<n; j++)
              memo[m-1][j] = 1;
          // Bottom up
          for(int i = m-2; i>=0; i-- )
              for(int j = n-2; j>=0; j-- )
                  memo[i][j] = memo[i][j+1] + memo[i+1][j];

          return memo[0][0];
      }
    • Top-down 
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      int uniquePaths(int m, int n) {
          vector<vector<int>> memo(m, vector<int>(n, -1));

          // 初始化第一行
          for (int i=0;i<m; i++)
              memo[i][0] = 1;
          // 初始化最左行
          for (int j=0; j<n; j++)
              memo[0][j] = 1;

          // top-down
          for (int i=1;i<m; i++)
              for (int j=1; j<n; j++)
                  memo[i][j] = memo[i-1][j] + memo[i][j-1];
          return memo[m-1][n-1];
      }

#303 Range Sum Query - Immutable

  • 描述
1
2
3
4
5
6
7
8
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

Example:
Given nums = [-2, 0, 3, -5, 2, -1]

sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

  • 逻辑

    从nums[i] 到nums[j] 元素累加就可以了。这种方法对于一条query，没问题。但是query一般频繁的。最好可以把结果提前计算出来，之后的query操作秩序做一次减法，便可以得到结果。所以使用DP。

    • 状态定义：mem[0]=0，mem[i]表示从第一个数到第i个数的和。
    • 状态转移方程：memo[i+1] = memo[i] + nums[i];
    • 初始化mem为全零。

  • 实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    class NumArray2{
        private:
            vector<int> memo;
        public:
            NumArray2(vector<int>& nums){
                // n+1个元素。
                memo = vector<int>(nums.size()+1, 0);

                for (int i=0; i<nums.size(); i++)
                    memo[i+1] = memo[i] + nums[i];
            }

            // 频繁操作只需求一次减法。效率高
            int sumRange(int i, int j){
                return memo[j+1] - memo[i];
            }
    };

#198 House Robber

  • 描述
1
2
3
4
5
6
一条街上有若干房子，现在要抢劫房子，从街头到街尾，所抢的房子不能直接相邻，求可能的最大收益。

Input: [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
             Total amount you can rob = 2 + 9 + 1 = 12.

  • 逻辑

    • 状态定义：mem[i]表示抢[0~i]可获得的最大收益。

    • 状态转移方程：memo[i] = max(memo[i-1], nums[i]+tmp;

      下图为抢house=[5,2,3,1,1,5]的DP过程：

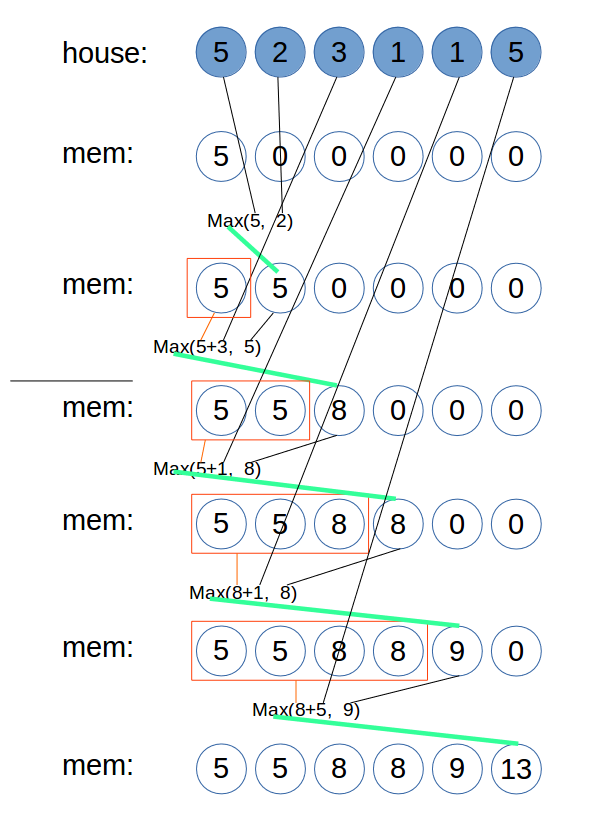
  • 实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    int rob(vector<int>& nums) {
        vector<int> memo(nums.size(), 0);
        
        // 切入口：前两个值特殊处理
        memo[0] = nums[0];  
        memo[1] = max(nums[0], nums[1]);
        
        // 开始切~~
        for (int i=2; i<nums.size(); i++){
            // 求tmp：当前位置之前可抢劫最大收益（不包括与当前位置紧邻的房子）
            int tmp=0;    
            for (int j=0; j<=i-2; j++)
                if (memo[j]>tmp)
                    tmp = memo[j];

            memo[i] = max(memo[i-1], nums[i]+tmp);
            
        }
        return memo[nums.size()-1];
    }

    关键：mem[],以初始化的值为切入点，一个一个计算。，