Machine Learning

回看SVM-(一)

写在前面

  • 支持向量：两类别距离决策边界最近且相等的点。
  • SVM目的：使得两个类别的SV间的距离最小。即最大化Margin间的距离。
  • SVM考虑当前样本同时，又考虑到未来可能出现的样本，即使找到的决策边界尽量有强的泛化能力。
  • 经过数学推到，可以将问题转化为最优化问题。如同其他参数学习算法。
  • 其他机器学习算法一般是全局最优化问题，而SVM是有条件的最优化问题。
  • 有条件的最优化问题使用拉格朗日算子求解。
  • KKT条件
  • Hard Margin要严格满足两个Margin见没有没有任何样本点。这由该最优化问题的条件决定。
  • Soft Margin允许两个Margin之间存在样本点，即有容错的能力。相应的模型条件与目标都会体现该容错能力。
  • L1正则；L2正则
  • Hinge损失函数，Exponential Loss，Logistic Loss，是常用的损失函数，由好的数学性质。
  • 惩罚项表达了容错空间，不能太大。
  • 目标表达式中的C，目的是平衡前后两部分的比例。
  • 此处C（正则化惩罚系数）与其他ML算法C含义不同，但是可以相同地解读。且C越大，越接近Hard Margin。
  • SVM中涉及距离，所以要对数据进行标准化处理。否则当不同维数的特征尺度不同时，影响模型性能。

1. 数据

有二分类样本：

1
2
3
4
5
6
7
8
iris = datasets.load_iris()

x = iris.data    # 150 x 4
y = iris.target  # 150

# 二分类模型
x = x[y < 2, :2]  # 100 x 2
y = y[y < 2]     # 100

2. 首先标准化处理：

1
2
3
4
5
from sklearn.preprocessing import StandardScaler

stand = StandardScaler()
stand.fit(x)
x_standard = stand.transform(x)

得到标准化后的x_standard。

为了说明问题，使用所有数据fit，使用原来数据predict。

3. 当C取很大值时，如C=1e9：

1
2
3
svc = LinearSVC(C=1e9)
svc.fit(x_standard, y)
y_predict = svc.predict(x_standard)

查看模型所学，w和b：

1
2
print(svc.coef_)       # w [[ 4.03242779 -2.49296705]] 
print(svc.intercept_)  # b [ 0.95365901]

绘出决策边界， 及两个Margin：

1
2
3
4
plot_svc_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(x_standard[y_predict==0,0], x_standard[y_predict==0,1])
plt.scatter(x_standard[y_predict==1,0], x_standard[y_predict==1,1])
plt.show()

如图：

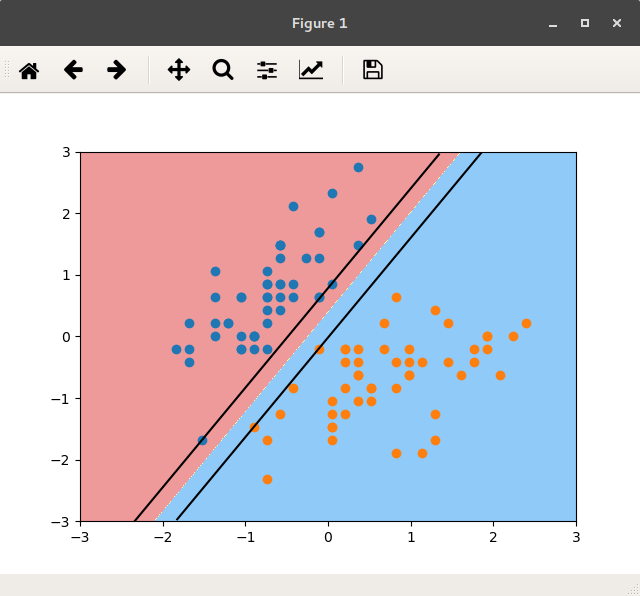
图 C=1e9的分类边界

4. 当C取很小值时，如C=0.05：

1
2
3
svc2 = LinearSVC(C=0.005)
svc2.fit(x_standard, y)
y_y_predict = svc2.predict(x_standard)

查看模型所学，w&b：

1
2
print(svc2.coef_)       # w [[ 0.33360588 -0.30904355]]
print(svc2.intercept_)  # b [  3.81794231e-08]

绘出决策边界，及两个Margin：

1
2
3
4
plot_svc_decision_boundary(svc2, axis=[-3, 3, -3, 3])
plt.scatter(x_standard[y_predict==0,0], x_standard[y_predict==0,1])
plt.scatter(x_standard[y_predict==1,0], x_standard[y_predict==1,1])
plt.show()

如图：

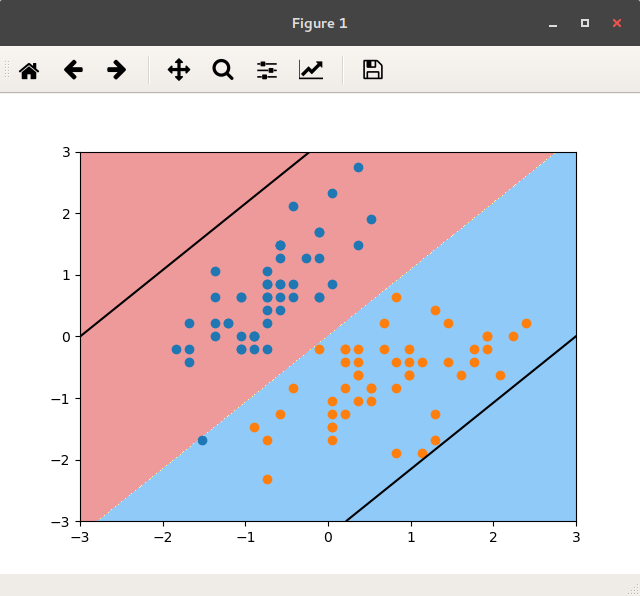
图 C=0.005的分类边界

当C太小时，容错空间太大，以至于大量明显分错的点也被模型认为是允许的。

这是当只指明C后，模型的参数：

1
2
3
4
LinearSVC(C=1000000000.0, class_weight=None, dual=True, f   it_intercept=True,
     intercept_scaling=1, loss='squared_hinge', max_iter=1000,
     multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
     verbose=0)

可以看出，使用的是hinge损失函数，L2正则化，ovr…等其他设置。

附件

绘出决策边界，及两个Margin的函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# show margins and boundary:
def plot_svc_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])

    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

    # margin lines:
    w = model.coef_[0]
    b = model.intercept_[0]

    # w0*x0 + w1*x1 + b = 0
    # => x1 = -w0/w1 * x0 - b/w1
    plot_x = np.linspace(axis[0], axis[1], 200)
    # # w0*x0 + w1*x1 + b = 1
    above_y = -w[0] / w[1] * plot_x - b / w[1] + (1 / w[1])
    # # w0*x0 + w1*x1 + b = -1
    below_y = -w[0] / w[1] * plot_x - b / w[1] - (1 / w[1])

    # two boolean vectors: set the length of lines
    above_index = (above_y >= axis[2]) & (above_y <= axis[3])
    below_index = (below_y >= axis[2]) & (below_y <= axis[3])
    plt.plot(plot_x[above_index], above_y[above_index], color='black')
    plt.plot(plot_x[below_index], below_y[below_index], color='black')