信息论-信息量与二叉树

香浓认为，对于一条信息，重要的是找出这条信息中含有多少信息量，要搞清楚信息量，就要找到一个量化度量信息的单位。香浓的最大贡献就是找到了这个单位“比特(bit)”。
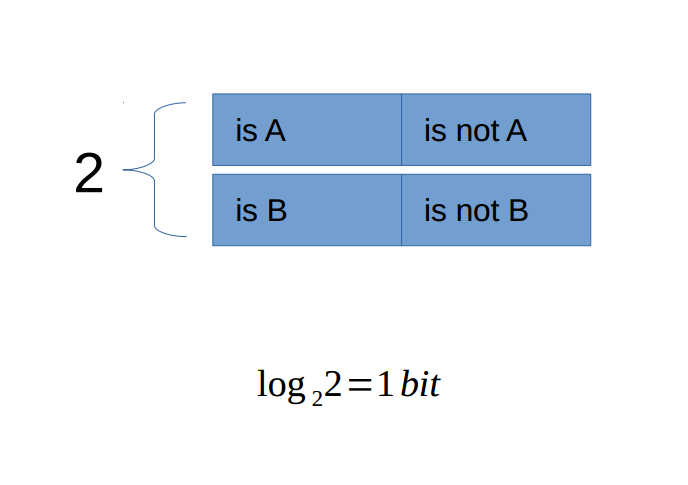
比特是度量信息量的基本单位。它可以被这样定义：如果一个黑盒子里由A和B两种可能，而且这两种可能出现的概率相同。那么要搞清楚黑盒子中到底是A还是B，所需要的信息量就是一个比特(bit)。
当A和B的出现的概率不相同时，确定他们谁出现所需的信息量就不到一个比特。

比如，设抛一枚两面质地均匀的硬币为一个系统，状态A和B分别是正面朝上和反面朝上。则确定一次投掷所需要的信息量为一个比特。
可以这样计算：

又比如，做一道4(有A,B,C,D4中状态)选一个的选择题，需要多少信息量才能找到正确答案。2bits。先使用1bit信息确定比如是否在A或B中，若是，再使用1bit信息量确定是否是A，若否，则最终答案是B。(这只是一种判断出结果的方法，但每种方法所需的信息量都是2bits)：

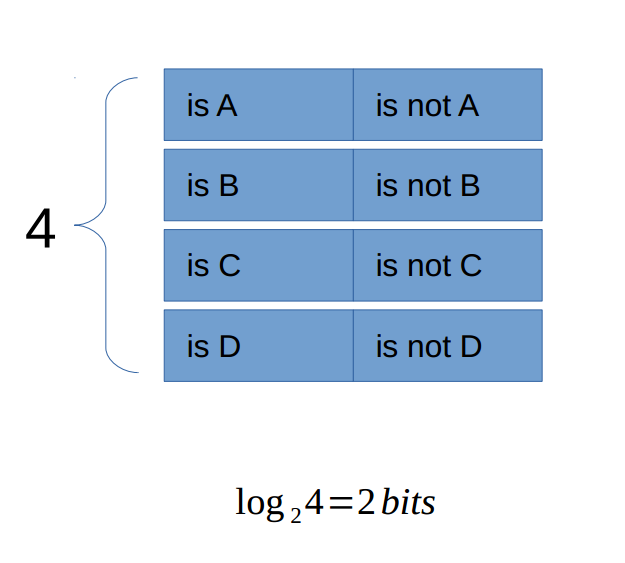
所以，如果由32个足球队参加世界杯，最终需要5bits的信息量确定最终哪支球队为冠军。

可以看出的规律：一棵树，以所有可能情况为根，平均分所有情况给左子右子，如此递归，直到每个叶节点只有一种情况。此时得到树的深度即为确定做种是哪种情况所需的信息量。以选择题为例：

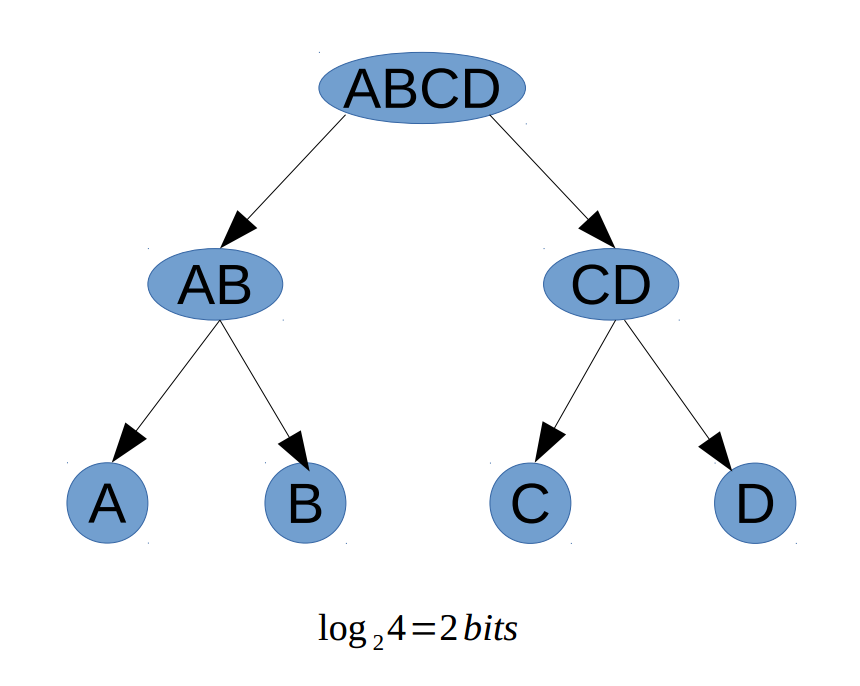
树的深度为2，从树根到树叶需要2步走，即需要2bits信息确定究竟是哪一个。

我们把充满不确定性的盒子称作“信息源”，它里面的不确定性称作“信息熵”，“信息”是用来消除这些不确定性的(信息熵)。所以要消除黑盒子里的不确定性，需要的“信息量”等于“信息熵”。“熵”是热力学的概念，它表示混乱程度，同样的，信息论中的信息熵表示一个系统中的不确定性。

一个系统中的状态数量也叫做可能性数量，越多，系统不确定性越大；当状态数量确定时，各个状态的可能性相同，熵达到最大；相反，如果只要概率有不相同，系统不确定性就会减小，极限情况下，当状态A发生的概率为99.9%，而其他所有状态发生的概率和为0.01%时，系统的不确定性很小：很大的概率上A是会发生的。香浓用以下公式可以计算出系统信息熵：

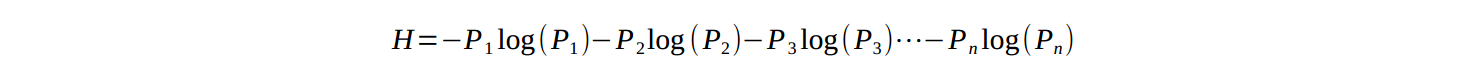
以二分类为例，下图体现了一个状态的概率与系统的信息熵的关系：

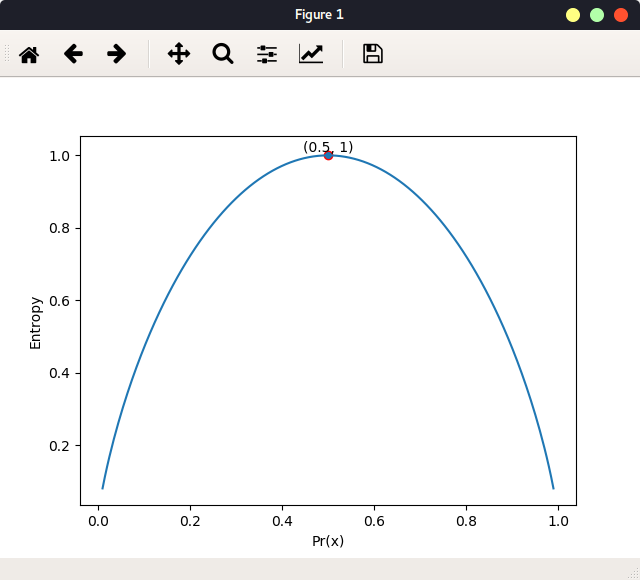
当状态概率为0.5时，系统信息熵，即不确定性达最大值。实现：

# 根据上述信息熵计算公式
def entropy(p):
    return -p * np.log2(p)-(1-p)*np.log2(1-p)

x = np.linspace(0.01, 0.99, 200)

plt.plot(x, entropy(x))
# 绘出一个点
plt.scatter([0.5], [1], marker='o', edgecolors='r')   
# 添加注释 
plt.text(0.5, 1, (0.5, 1), ha='center', va='bottom', fontsize=10)   
plt.xlabel('Pr(x)', fontsize=10)
plt.ylabel('Entropy', fontsize=10)
plt.show()

在构建ID3决策树时，就是根据信息熵公式，得到各种划分后的信息熵，选取信息熵最小的划分。即这个划分使得系统不确定性变得最小！

如四选一选择题，假如，每种选项的概率均为0.25，根据公式，消除选择题的不确定性所需信息量为2bits。
如果4中选项的概率不相同，不论哪种情况，信息熵均小于2bits。

通过平衡二叉树来理解信息量单位比特。如果一个分类模型在一个数据集上的正确率为0.5，那么可以说，这个模型是最糟糕的模型，它对减少系统信息熵没有贡献。

补充

热力学熵和信息熵的物理意义，数学形式，完全一样，不存在本质区别，只是应用领域不同。克劳修斯形式(熵的宏观形式)用于内燃机研究，进入量子时代后主要使用玻尔兹曼形式(熵的微观形式)。
玻尔兹曼熵与信息熵的唯一不同只是前者计算对数用e为底数得到单位为nats，后者计算使用2为底数得到单位为bit。

另外，取10为底，得到单位是bans。其实，在决策树的计算中，求信息熵的对数底可以使任意的，因为具体在划分的时候，不管底取多少，H这个函数的性质是不会变的。模型其实在意熵的相对值，而非绝对值。

熵增原理：任何孤立的系统，总熵不会减少。