Machine Learning

回看SVM-(三)

升维

在现实任务中，样本空间内很可能不存在一个能将样本正确划分的超平面。此时，可以将样本从原始空间映射到一个更高维的样本空间，使得样本在这个高维空间内线性可分。如果原始空间是有限维的，也就是说，样本的属性个数有限，那么一定存在一个更高的样本维度使样本线性可分。

上述涉及到每一个特征映射到高维空间后之间的内积，由于特征空间的维度可能很高，甚至是无穷维的，因此先映射到高维空间后计算，是非常困难的。即，核函数可以等价代替样本映射后的特征向量间的内积。使用Kernel Trick 避开这个障碍。如此用一个近似的计算来取代映射到高维特征向量。好处：减少了计算量，节省了内存，Kernel Trick是一个可以应用于任何算法的技巧。

RBF核

假如原始数据只有一维信息，如果有两个landmark，就将数据变化为2维数据。每个样本的取值变化为x->( ，)，即含有2个特征。下面模拟该过程： 

1
2
3
4
5
6
7
8
9
# 一维数据x
x = np.arange(-10, 10, 1) 

# 对应的lable
y = np.asarray((x >= -3) & (x <= 3), dtype=int)

plt.scatter(x[y == 0], 0*(y[y == 0]))
plt.scatter(x[y == 1], 0*(y[y == 1]))
plt.show()

如图：

图 原始数据

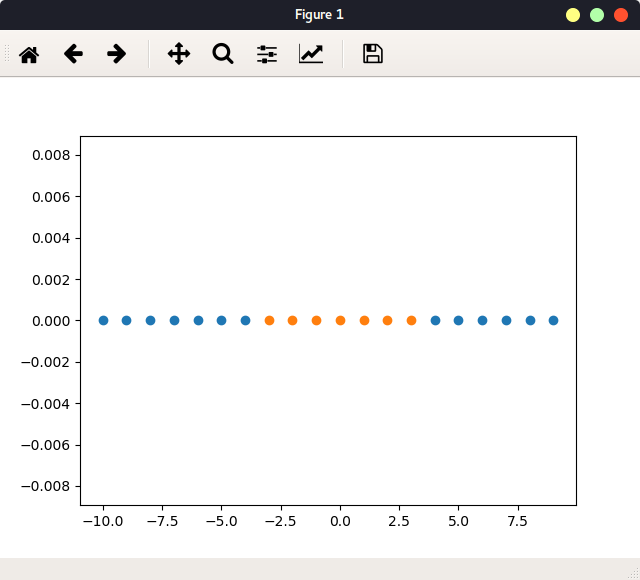
定义一个函数，每个样本跟landmark进行计算，得到新的x：

1
2
3
4
5
6
7
8
9
def gaussian(x, l):
    """
    每个x 跟l计算得到新的x
    :param x: 原来x
    :param l: x跟谁计算
    :return: 新的x
    """
    gamma = 0.05
    return np.exp(-gamma * (x - l)**2)

对x的每个样本进行升维处理，得到新的x：

1
2
3
4
5
6
7
8
9
10
11
x_new = np.empty((len(x), 2))

for i, data in enumerate(x):
    # x_new 的第一个特征：
    x_new[i, 0] = gaussian(data, 1)
    # x_new 的第二个特征：
    x_new[i, 1] = gaussian(data, -1)

plt.scatter(x_new[y == 0, 0], x_new[y == 0, 1])
plt.scatter(x_new[y == 1, 0], x_new[y == 1, 1])
plt.show()

如图：

图 升维后的数据

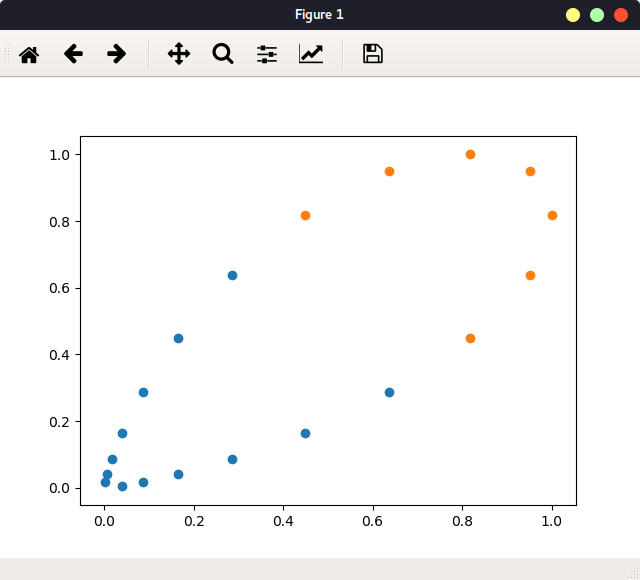
此2维数据显然是线性可分的。本例是使用l1和l2 两个landmark，即，只将数据变化为2维，原本20x1的数据映射成20x2。BRF高斯核实际上是使用每一个数据点作为landmark，即原本mxn的数据映射成mxm的数据。当m远远大于n时(一般合格的数据集)，数据特征由n增加到m。当然，对于一个m小于n的数据集(如NLP等情境下的数据)，依然变换为mxm，其实是降维处理。

RBF核gamma

RBF中的参数gamma与高斯分布有关：gamma越大，分布越窄越高。
实验如下：

1
2
3
4
5
6
7
# 使用moon数据：
x, y = datasets.make_moons(noise=0.15, random_state=11)

# 定义模型：
def RBFKernel(gamma=0.1):
    return Pipeline([("standard", StandardScaler()),
                     ("svc", SVC(kernel="rbf", gamma=gamma))])

指定gamma，并学习，当gamma=100时：

1
2
3
4
5
6
svc = RBFKernel(100)
svc.fit(x, y)
plot_decision_boundary(svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y == 0, 0], x[y == 0, 1])
plt.scatter(x[y == 1, 0], x[y == 1, 1])
plt.show()

绘图：

图 gamma=100

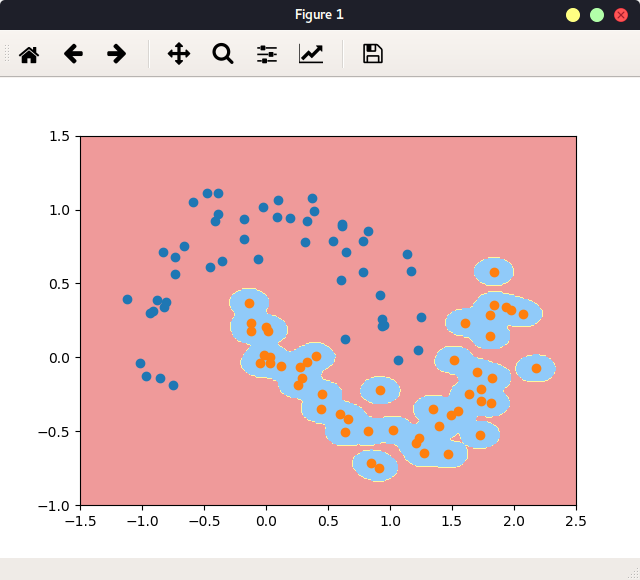
当gamma=100，很大， 对应高斯分布越高越窄， 反映在图中就是每一个橘色样本点周围的小区域为一个高斯分布，橘色样本点本身为分布的顶点，即，模型判断，样本点只在这样一个区域内，才被判定为橘色点。 此情况显然过拟合。

当gamma=10， 上述的分布区域变大了：

图 gamma=10

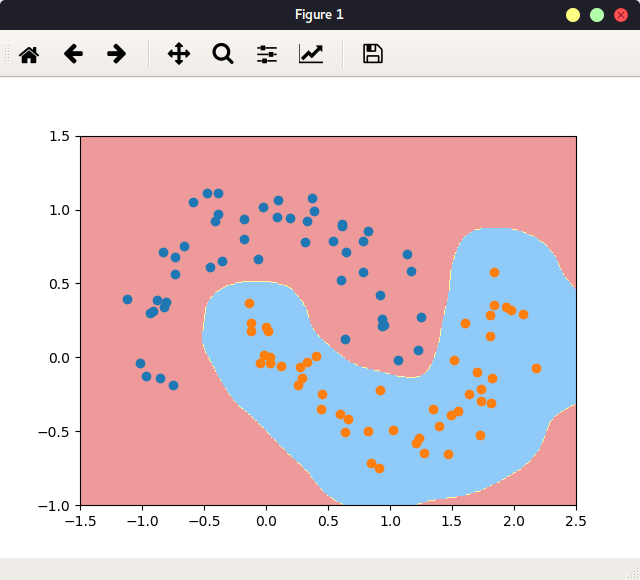
当gamma=0.1，很小时，不拟合：

图 gamma=0.1

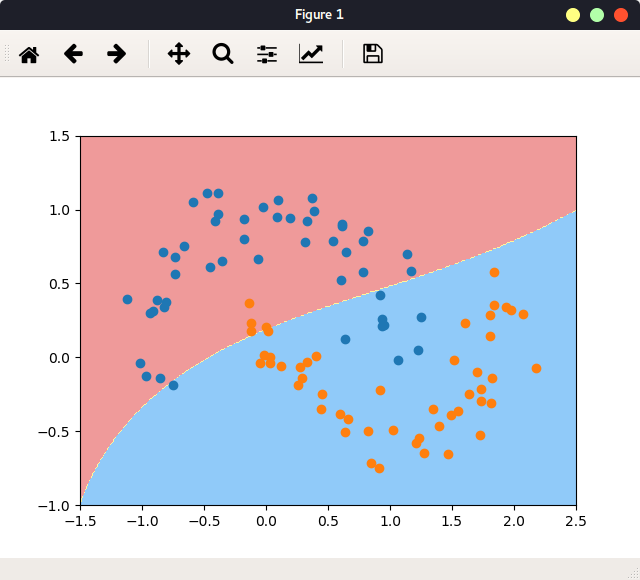
所以可以说，gamma值在控制模型的复杂度，gamma越小，模型复杂度越小，
所以要找到合适的gamma。

SVM解决回归问题：SVR

SVR 使得在margin范围里的样本点越多越好，表示这个范围可以较好地表示样本点。此时取中间的线为回归曲线。

或者说，SVR解决的问题与SVM相反，soft SVM要使得margin间的点越少越好，而SVR要使得margin间的点越多越好。

又或者说，SVR目的与SVM相同，都是最大化margin间的距离。SVR假设我们可以容忍f(x)与y之间最多有epislon的偏差，即，当且仅当f(x)与y之间的距离绝对值大于epsilon时，才计算损失，损失仍是最小化margin间的距离。这个过程相当于构建了宽度为2×epsilon的间隔带，如果样本点在间隔带之间，则认为是被预测正确的。

sklearn中的使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sklearn.svm import LinearSVR
from sklearn.svm import SVR  # 指明核函数
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline


def StandardLinearSVR(epsilon=0.1, c=1):
    """
    指明参数 epsilon 和 C 等
    """
    return Pipeline([
        ("standard", StandardScaler()),
        ("LinearSVR", LinearSVR(epsilon=epsilon, C=c))
    ])