Machine Learning

回看SVM-(二)

对于线性不可分而非线性可分的数据，也可以使用线性SVM。只需要将数据转换为高维的含有多项式项的数据。

数据集

先找一个，分线性可分数据集：

1
2
3
4
5
6
7
8
from sklearn import datasets

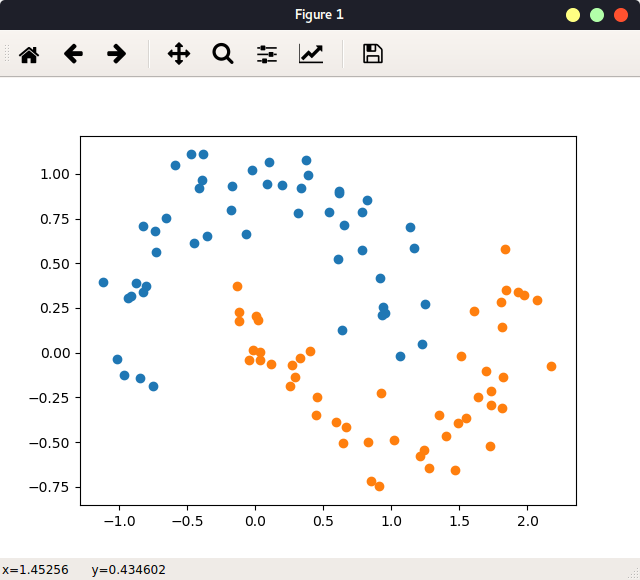
x, y = datasets.make_moons(noise=0.15, random_state=11)

# 绘制出结果：
plt.scatter(x[y==0, 0], x[y==0,1])
plt.scatter(x[y==1, 0], x[y==1,1])
plt.show()

结果：

图 待处理数据

含多项式特征的LinearSVM

指定多形式的阶数，将数据转化成高维的含有多项式项数据，后传入LinearSVM：

1
2
3
4
5
6
def PolynomialSVC(degree, C=0.1):
    return Pipeline([
        ("Poly", PolynomialFeatures(degree=degree)),
        ("standard", StandardScaler()),
        ("LinearSVC", LinearSVC(C=C))
    ])

使用Pipline可以顺序执行各部分。实例化模型，并查看模型信息：

1
2
3
poly_svc = PolynomialSVC(3)
poly_svc.fit(x, y)
print(poly_svc)

模型信息：

1
2
3
4
5
Pipeline(memory=None,
     steps=[('Poly', PolynomialFeatures(degree=3, include_bias=True, interaction_only=False)), ('standard', StandardScaler(copy=True, with_mean=True, with_std=True)), ('LinearSVC', LinearSVC(C=0.1, class_weight=None, dual=True, fit_intercept=True,
     intercept_scaling=1, loss='squared_hinge', max_iter=1000,
     multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
     verbose=0))])

绘出分类边界：

1
2
3
4
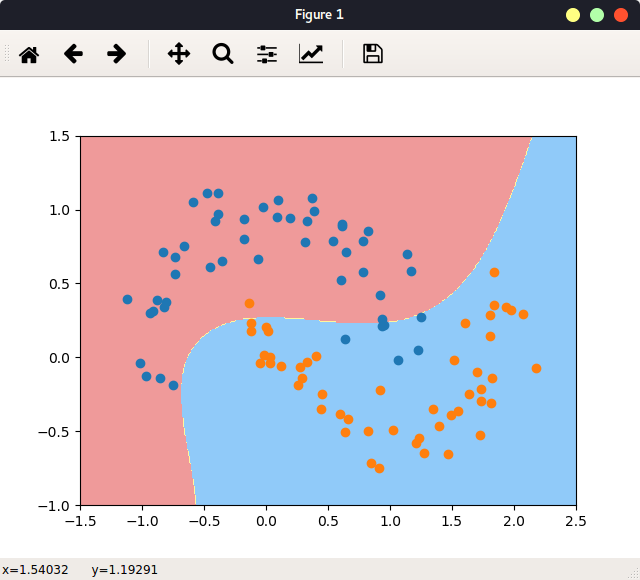
plot_decision_boundary(poly_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y==0, 0], x[y==0,1])
plt.scatter(x[y==1, 0], x[y==1,1])
plt.show()

结果为分线性边界：

图 分类边界

多项式核函数

SVM可以直接使用数据的多项式特征，即多项式核函数，所以使用SVC而非LinearSVC。此时Pipline中不需先得到多项式特征：

1
2
3
4
5
6
7
from sklearn.svm import SVC

def Polynomial_KernelSVC(degree, C=0.1):
    return Pipeline([
        ("standard", StandardScaler()),
        ("kernelSVC", SVC(kernel="poly", degree=degree, C=C))  
    ])

传入kernel参数，指定使用什么样的核函数。实例化模型，绘制分类边界：

1
2
3
4
5
6
7
poly_kernel_svc = Polynomial_KernelSVC(degree=5)
poly_kernel_svc.fit(x, y)

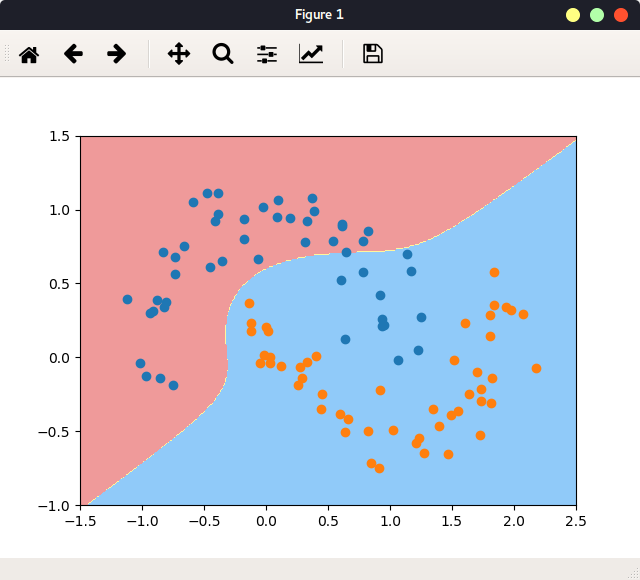
plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y==0, 0], x[y==0,1])
plt.scatter(x[y==1, 0], x[y==1,1])
plt.show()

边界：

图 使用多项式核函数的分类边界