Machine Learning

回顾决策树(一)

  • 决策树是非参数学习算法
  • 天然解决多分类问题
  • 有很好的可解释性
  • 关键问题是使用哪个特征做为根节点
  • 对于连续值的特征，在哪个值上做划分

离散数据集

使用iris数据集，调用sklearn的Decision Tree 模型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
iris = datasets.load_iris()

# 只是用数据2个特征
x = iris.data[:, 2:]
y = iris.target

from sklearn.tree import DecisionTreeClassifier

tree_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy")
tree_clf.fit(x, y)

plot_decision_boundary(tree_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(x[y == 0, 0], x[y == 0, 1])
plt.scatter(x[y == 2, 0], x[y == 2, 1])
plt.scatter(x[y == 1, 0], x[y == 1, 1])
plt.show()

结果：

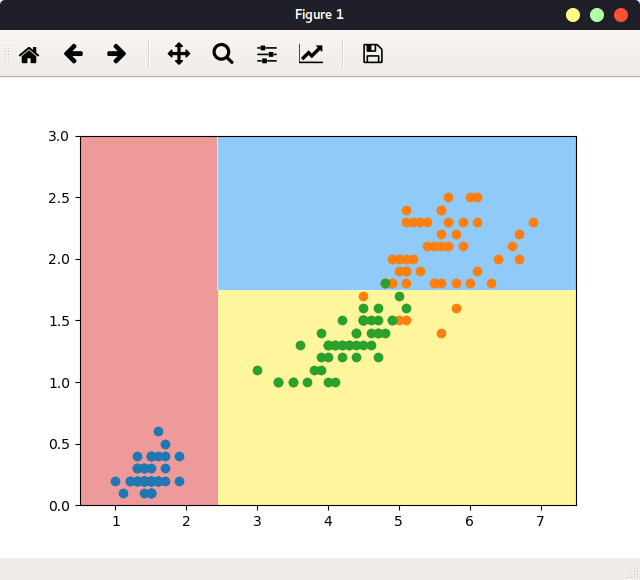
图 深度为2的决策树

划分后使得系统的熵（即不确定性）降低。所以对于一个划分，如果划分后的系统信息熵比其他划分后的熵都要小，则当前就是用这个划分。根据这个原理，可以就特征为连续值的数据集进行划分：

连续值的数据集

已知特征d，和value， 对x进行划分：

1
2
3
4
def split(x, y, d, value):
    index_a = (x[:, d] <= value)
    index_b = (x[:, d] > value)
    return x[index_a], x[index_b], y[index_a], y[index_b]

传入label列表，求此时的系统信息熵：

1
2
3
4
5
6
7
8
9
10
11
from collections import Counter
from math import log2

def cal_entropy(y):
    # counter 为字典，[类别，这个类别所含样本数]
    counter = Counter(y)  
    res = 0.0
    for num in counter.values():
        p = num / len(y)
        res += -p * log2(p)
    return res

定义一次划分，即，划分算法：搜索找到使得熵最小的特征d和value：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def try_split(x, y):

    # 初始值最大
    best_entropy = float('inf')  
    # best_e_l, best_e_r = -1, -1
    # 初始化d 和 value
    best_d, best_v = -1, -1   
    # 在x 的所有维度（特征）搜索d：
    for d in range(x.shape[1]):
        # 在特征d的哪个值上划分：先排序，后找相邻的样本在特征d上的中间值是多少
        sorted_index = np.argsort(x[:, d])
        for i in range(1, len(x)):  # 遍历所有样本
            if x[sorted_index[i-1], d] != x[sorted_index[i], d]:
                v = (x[sorted_index[i-1], d] + x[sorted_index[i], d]) / 2
                # 有了 d 和 v， split：
                x_l, x_r, y_l, y_r = split(x, y, d, v) 
                # 此时系统熵是多少
                e = cal_entropy(y_l) + cal_entropy(y_r)
                # e_l = cal_entropy(y_l)
                # e_r = cal_entropy(y_r)
                # 判断新的熵e是否小于best_entropy，更新best_entropy
                if e < best_entropy:
                    best_entropy, best_v, best_d = e, v, d

    return best_entropy, best_d, best_v

调用函数得第一次划分：

1
2
3
4
5
6
# 第一次划分：
best_entropy, best_d, best_v = try_split(x, y)
x1_l, x1_r, y1_l, y1_r = split(x, y, best_d, best_v)

print(cal_entropy(y1_l))  # 0.0  
print(cal_entropy(y1_r))  # 1.0

左子树的熵为0，右子树的熵大于0，所以对右子树进行第二次划分：

1
2
3
4
5
6
# 对于右边再次划分：
best2_entropy, best2_d, best2_v = try_split(x1_r, y1_r)
x2_l, x2_r, y2_l, y2_r = split(x1_r, y1_r, best2_d, best2_v)

print(cal_entropy(y2_l))  # 0.44506485705083865
print(cal_entropy(y2_r))  # 0.15109697051711368

可以继续深入划分。

由于数据集各个特征值是连续的，所以，上述过程是：遍历找到所划分的特征，这个特征中遍历的所有样本，排序后求相邻两个样本的均值作为这个特征的具体划分值，时间复杂度为O(mxn)，即样本个数乘以特征个数。

对于各个特征值为离散的，使用信息增益来找到消除不确定性最强的特征。每次都找信息增益最大的属性作为下一个划分属性。