LeetCode

LeetCode-方法论-回溯法

46, 77, 40, 515,

  • 回溯法解决一类问题，排列与组合。
  • 属于树型问题，所以通常需要画递归树。
  • 通常需要有个容器来保存状态。
  • 实现方法：理解问题，画递归树。
  • 递归实现，需要“跳进跳出”的思维
  • 分清楚操作部分和结点移动部分
  • 一个模式：移动控制+结点操作 对上一条的强调

#46

  • 描述

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    给出一组不重复的整数，返回所有排列。如：
    Input: [1,2,3]
    Output:
    [
    [1,2,3],
    [1,3,2],
    [2,1,3],
    [2,3,1],
    [3,1,2],
    [3,2,1]
    ]

  • 逻辑

    每一种排列包含3个元素，思路很直接：构建一棵树，树的结点表示形成的一个组合，叶节点表示一个完整的组合。过程中需要一个容器来记录每一个叶节点，即一个排列。还需要一个布尔型容器来记录已经处理过的元素。最后还需要一个容器记录所有找到的排列，即最终返回的结果。过程可以用一棵树的先序遍历完成：

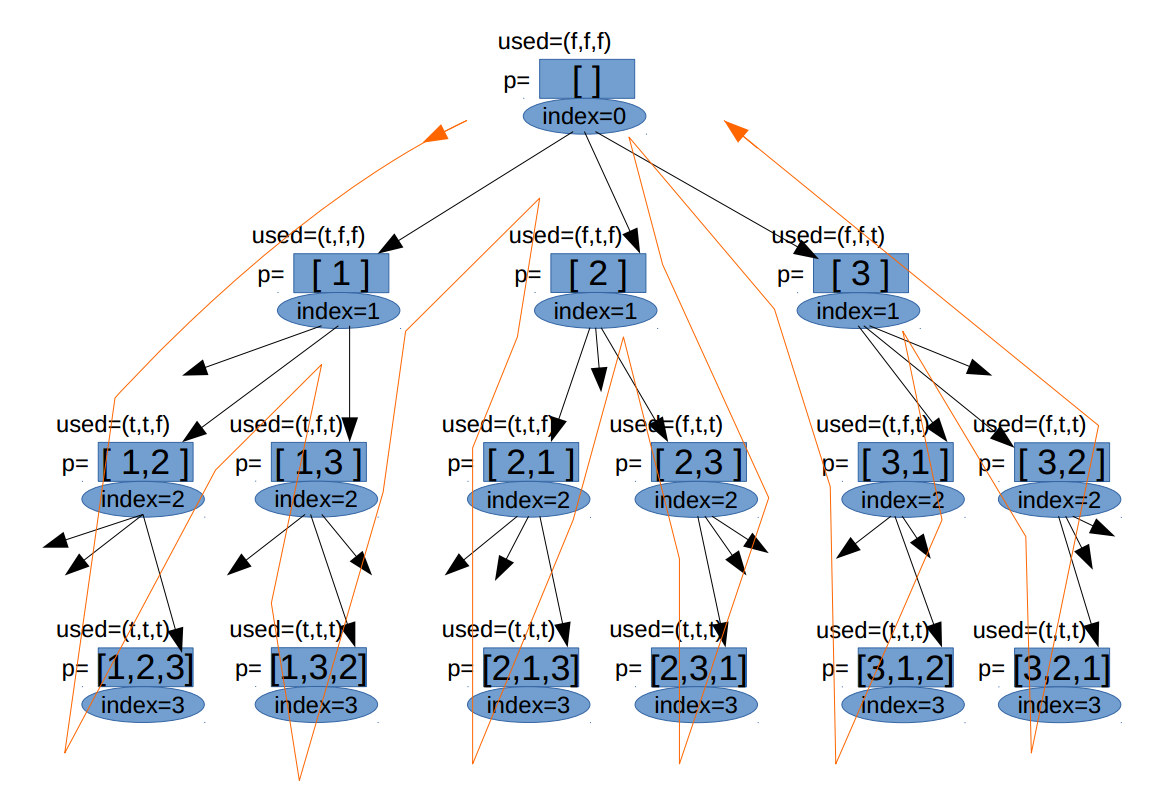
    图中橘红色箭头表示程序执行过程。体会递归“跳进跳出”的执行方式，每到“触底反弹”，便体现了回溯的“回”，所有变量值均回到上一层。递归算法很”整齐”，所有结点执行相同的操作。

  • 实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    // res 记录所有排列，最终返回res
    vector<vector<int>> res;
    // used 记录检查过的元素
    vector<bool> used;

    // 这个函数找到一个排列, num是输入，index表示当前考察元素的Index，p表示逐渐形成的一个排列
    // 向这个排列的末尾添加第index个元素，获得一个有Index个元素的排列。
    void getPermutaion(const vector<int>& nums, int index, vector<int>& p){

        // 递归到底的情况，所有元素都考察过之后。
        if (index == nums.size()){
            res.push_back(p);
            return;
        }

        // 以每一个元素作为这棵树的根：
        for (int i=0; i<nums.size(); i++){
            // 只有当元素没有考察过，才执行以下
            if (used[i] == false){
                used[i] = true;        //
                p.push_back(nums[i]);   // 把这个元素放入p中
                getPermutaion(nums, index+1, p);   // 形成这棵树的子树
                p.pop_back();    // 这里体现了回溯的“回”，回到上一步
                used[i]=false;   // 回到上一步
            }
        }
        return ;
    }

    // 入口函数
    vector<vector<int>> permute(vector<int>& nums) {
        used = vector<bool>(nums.size(), false);
        vector<int> p;
        getPermutaion(nums, 0, p);
        return res;
    }

    敲黑板

  1. 思维：跳进跳出
  2. 实现：跳进跳“回”
  3. 明确(写出)结点函数的定义，并且保持整个过程定义不变。

组合问题

#77

  • 描述：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    从n个数中取k个数，一共有哪些组合：
    Input: n = 4, k = 2
    Output:
    [
    [2,4],
    [3,4],
    [2,3],
    [1,2],
    [1,3],
    [1,4],
    ]

  • 逻辑

    分析问题：
    开始，根节点中不存在任何值，它的子节点从1开始遍历，形成组合中的第一个值[1], [2], [3], [4]。
    当结点第一个值为1时，它的子节点从2开始向后遍历。形成的组合有[1,2], [1,3], [1,4]。
    当结点第一个值为2时，其子节点从3开始遍历。得到组合[2,3], [2,4]。
    当结点第一个值为3时，其子节点从4开始遍历。得到组合[3,4]。
    当结点第一个值为4时，4超过了索引0~3，返回到根节点。

    给出递归树：

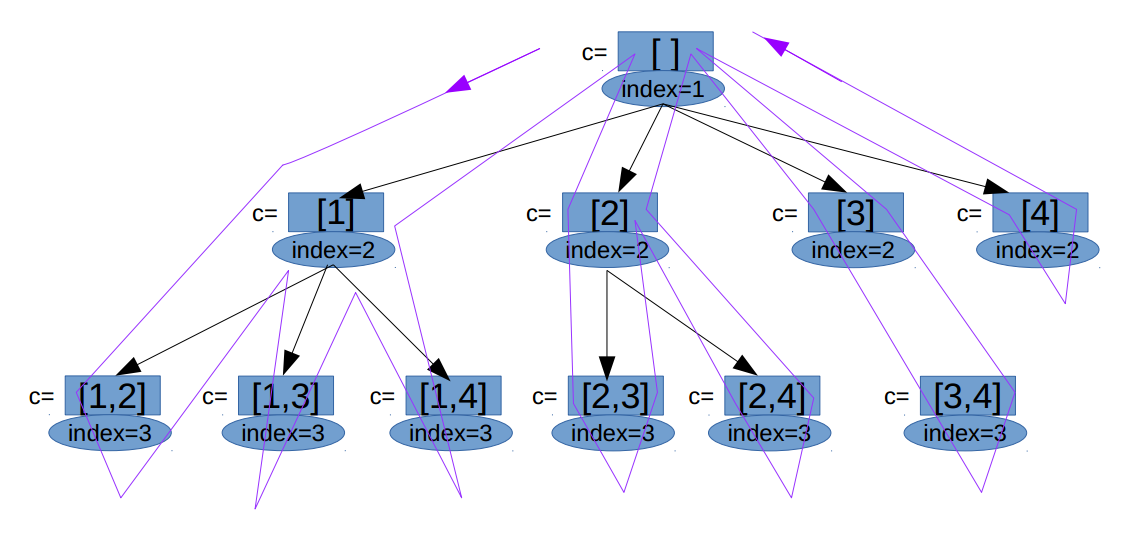
  • 实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    // res保存所有的组合
    vector<vector<int>> res;

    // 定义：从n个数中取k个数，把当前的数值放入c中，从Index开始向后查找：
    void generatCombination(int n, int k, int index, vector<int>& c){
        // 当c的大小为2时，表示找到一个组合
        if (c.size()==k){
            res.push_back(c);
            return;
        }

        // 
        for (int i=index; i<n; i++){
            c.push_back(i);
            // 以当前结点为根，从index+1开始向后找：
            generatCombination(n, k, index+1, c);
            c.pop_back();   // 回溯的“回”，跳回上一层。
        }
        return;
    }

    vector<vector<int>> combination(int n, int k){
        if (n<k || n<=0||k<=0 )
            return res;
        vector<int> c;
        // 从根节点开始，
        generatCombination(n, k, 1, c);
        return res;
    }

    这个问题的实现中，在递归函数里的for循环，循环变量i与index有关，表示从Index后查找，这保证了，组合中元素无重复，且组合无重复。这也是与上一个问题不同之处。可以回过去看排列问题，其递归函数中for循环i与Index无关，表示，i每次从0开始查找，使得每个排列中元素不必只是递增，就是说像[3,2,1]，也是一个排列。

敲黑板体会递归函数中for循环循环变量与index有关，无关的不同。

#40. Combination Sum II

  • 描述

    1
    2
    3
    4
    5
    6
    Input: candidates = [2,5,2,1,2], target = 5,
    A solution set is:
    [
    [1,2,2],
    [5]
    ]

  • 思路

    感觉上，需要回溯，所以先画出递归树：

    假设candidate=[1,2,3,4,5], target=5。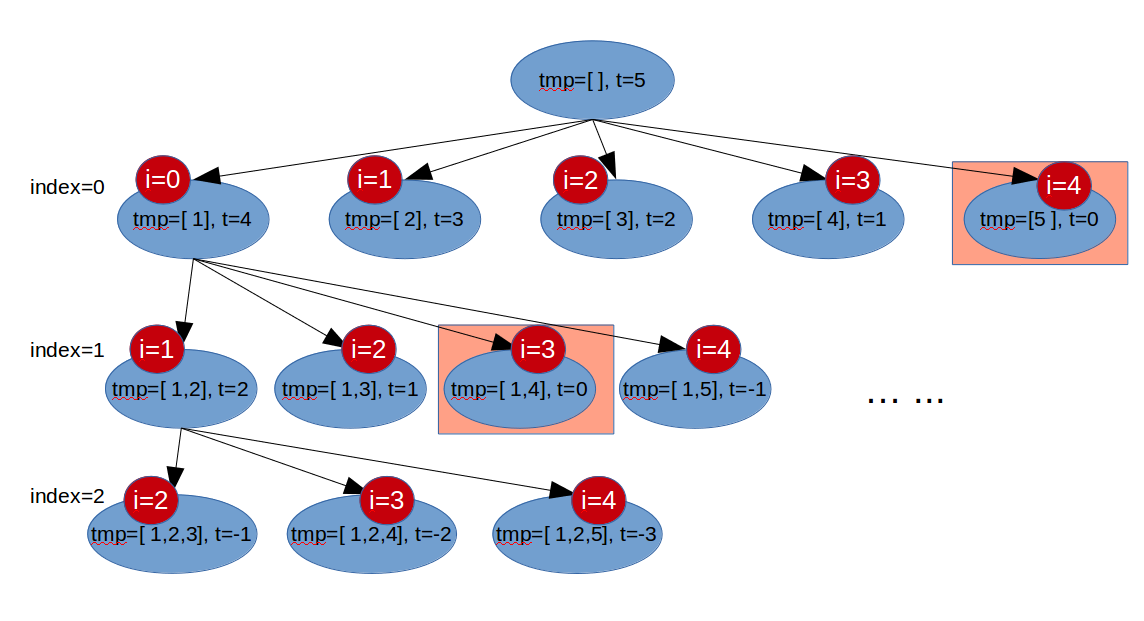

  • 实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target){
        set<vector<int>> res;
        vector<int> tmp;   // res中的每个元素
        sort(candidates.begin(), candidates.end());
        DFS(candidates, target, res, tmp ,0);
        return {res.begin(), res.end()};

    }

    // 每一个结点的操作
    void DFS(vector<int>& candidates, int target, set<vector<int>>& res, vector<int>& tmp, int index){
        if (target==0){   // 如果最后剩下为0，则表示找到一个sum为target
            res.insert(tmp);
            return;
        }

        for (int i=index; i<candidates.size(); i++){
            if (candidates[i]<=target){
                tmp.push_back(candidates[i]);
                DFS(candidates, target-candidates[i], res, tmp, i+1);
                tmp.pop_back();
            }else break;
        }
    }

    敲黑板一定要先画递归树，后写code，试图从别人的code中画递归树，是很容易懵掉的。

#515 Find Largest Value in Each Tree Row

  • 描述

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    You need to find the largest value in each row of a binary tree.
    Example:

    Input: 

            1
            / \
            3   2
        / \   \
        5   3   9 

    Output: [1, 3, 9]

  • 逻辑

    先画二叉树，见下图。

    本质是二叉树的遍历，先序遍历，顺序为下图中粉色箭头。而对于每个结点的操作是下图中橙色箭头。每个操作改变的是res数组，根据res的长度与row的索引决定。

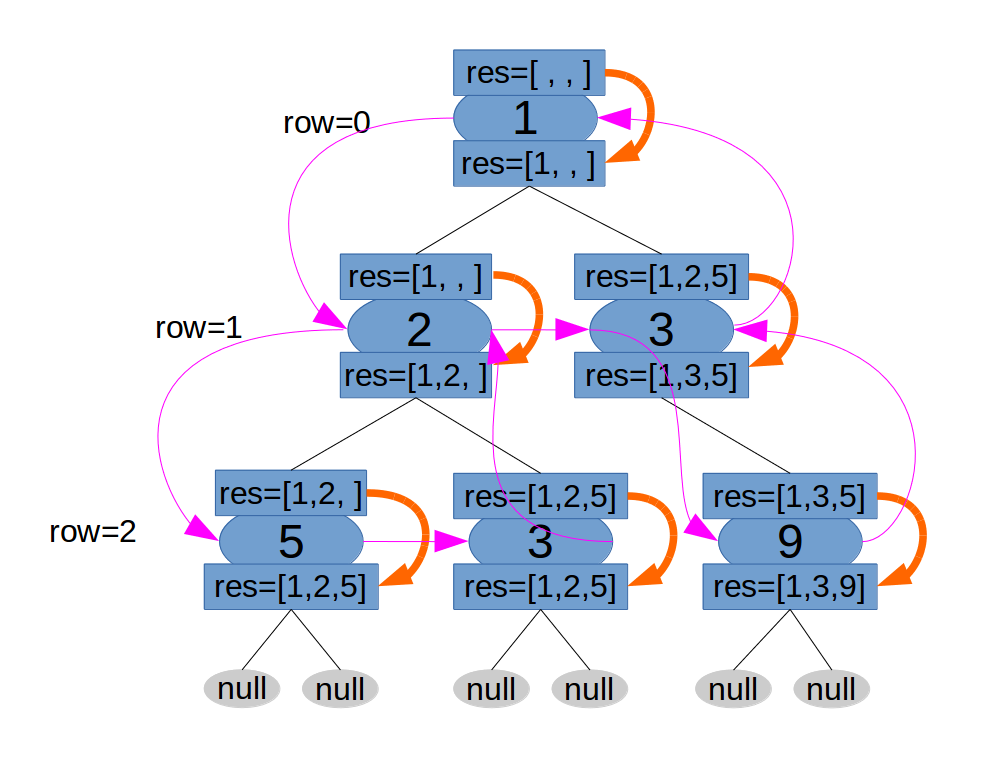
  • 实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    vector<int> largestValues(TreeNode* root){
        vector<int> res;
        DFS(root, 0, res);
        return res;
    }

    void DFS(TreeNode* root, int row, vector<int>& res){
        // operation ORANGE
        if (!root) return;

        if (row >= res.size())
            res.push_back(root->val);
        else
            res[row] = max(res[row], root->val);

        // move PINK
        DFS(root->left, row+1, res);
        DFS(root->right, row+1, res);
        return;
    }

关键： 变量row的跳进跳出,分清楚操作部分和结点移动部分

#17 Letter Combinations of a phone number

#491 All increasing Sub-sequences