接着记录数组相关问题。
56, 74, 240, 136, 1122, 1009, 868, 985,
常用技术:
- 粗调+精调
- XOR性质
- 额外变量的使用
- 数进制间的对应(相互为等价信息)
- 移位操作
- 首先想到的方法不是好的方法
#56 Merge intervals 合并区间
描述
1
2
3Input: [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].思路
第一步:按区间左边界排序 第二步:把第一个interval[0]放入结果容器res中,从第二个interval[1]开始: 如果interval[1]的左边界 >= res的最后一个interval的右边界,表示两者无交集, 把interval[1] append到res中; 如果interval[1]的左边界 < res的最后一个interval的右边界,表示两者有交集, 把interval[1]的右边界写入res最后一个interval的右边界。第二步过程间下示意图:
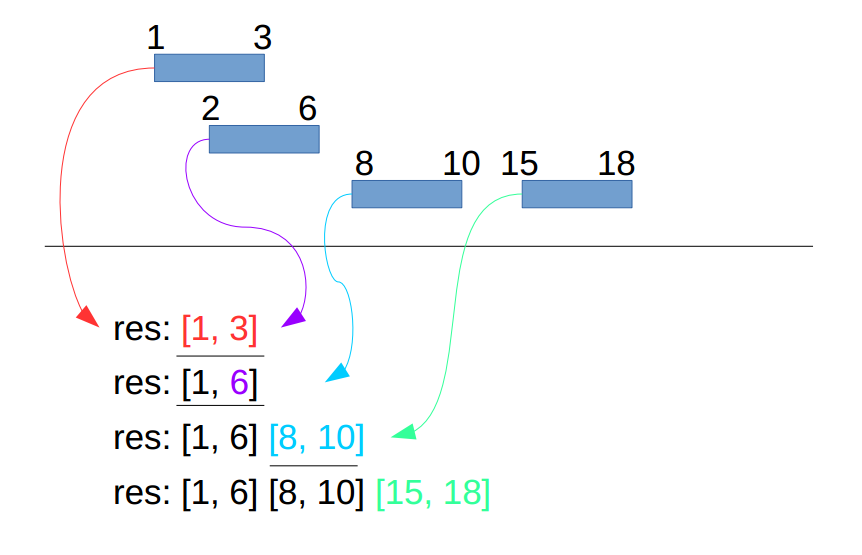
看图说话实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31static bool compare(vector<int>& a , vector<int>& b){
return a[0] < b[0];
}
vector<vector<int>> merge(vector<vector<int>>& intervals) {
vector<vector<int>> res;
if (intervals.size()==0)
return res;
if (intervals.size()==1){
res.push_back(intervals[0]);
return res;
}
// 区间左端点从小到大排序
sort(intervals.begin(), intervals.end(), compare);
res.push_back(intervals[0]);
int i=1;
while(i < intervals.size()){
vector<int>& last = res.back(); // 注意
if (last[1] < intervals[i][0]){
res.push_back(intervals[i]);
}else{
last[1] = max(last[1], intervals[i][1]);
}
i++;
}
return res;
}
关键: vector<int>& last = res.back(); 定义last 的类型是reference。由逻辑,凡是last被修改,就是res.back()被修改,所以last和res.back()为一个对象。
#64 Search 2D matrix
描述
1
2
3
4
5
6
7
8
9
10
11Input:
matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]
target = 16
Output: true
1.Integers in each row are sorted from left to right.
2.The first integer of each row is greater than the last integer of the previous row.思路
根据问题的特点,设计
粗调+精调方法:粗调:把每一行的最后一个元素放入新的数组中(m长度): [7, 20, 50]. 用target与其中的每个元素比较,找到第一个比target大的元素并返回index。 如:20 是第一个大于target的元素,返回1,即target在index=1的行。 精调:在index=1的行中搜索target。
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26bool searchMatrix(vector<vector<int>>& matrix, int target){
int row = matrix.size();
int col = matrix[0].size();
vector<int> station(row, 0);
for (int r=0; r<row; r++)
station[r] = matrix[r][col-1];
// rough-tuning
int pr = 0;
for (int i=0; i<station.size(); i++){
if (target == station[i])
return true;
if (target < station[i]){
pr = i;
break;
}
}
// fine-tuning
for (int c=0; c<col; c++){
if (matrix[pr][c] == target)
return true;
}
return false;
}关键: 粗调&精调
#240 Search 2D matrix II
描述
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17Consider the following matrix:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
Given target = 5, return true.
Given target = 20, return false.
1.Integers in each row are sorted in ascending from left to right.
2.Integers in each column are sorted in ascending from top to bottom.思路
与#74不同,对于方阵,可以使用粗调精调,但是对于非方阵,此法复杂。考虑新的方法,如下图:
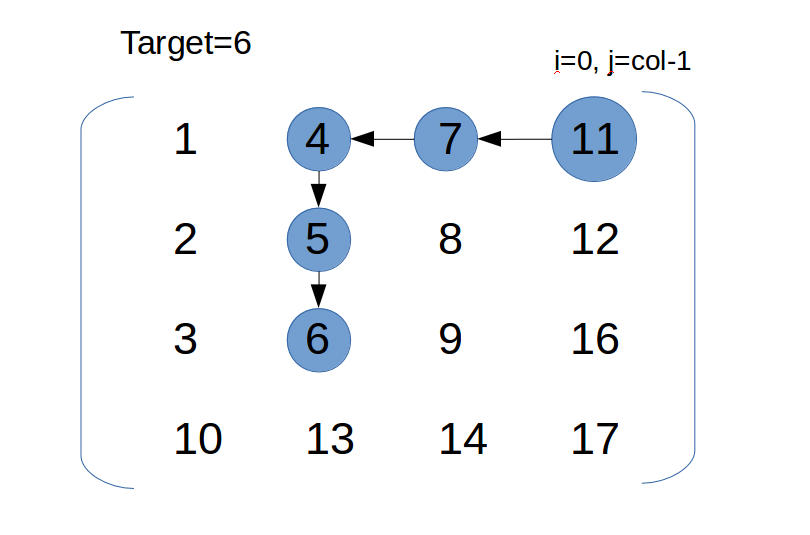
从右上角或(左下角开始),target与所到元素比较:
if (target > matrix[i][j]) i++; // 向下走 else if (target < matrix[i][j]) j--; // 向右走 else if(target == matrix[i][j])return true // 找到看图说话
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20bool searchMatrix(vector<vector<int>>& matrix, int target) {
int row = matrix.size();
if (row == 0)
return false;
int col = matrix[0].size();
if (col == 0)
return false;
if (target < matrix[0][0] || target > matrix[row-1][col-1])
return false;
int r = row-1;
int c = 0;
while(r >= 0 && c < col ){
if (target == matrix[r][c]) return true;
else if (target > matrix[r][c]) c++;
else r--;
}
return false;
}
#136 Single Number
描述
1
2
3
4
5Given a non-empty array of integers, every element appears twice
except for one. Find that single one.
Input: [4,1,2,1,2]
Output: 4思路
方法一: map
方法二: set
方法三: XOR 使用XOR的数学性质,可以很快地解决问题XOR 数学性质 I) a^0=a (a!=0) II) a^a=0 (a!=0) III) a^b^a = a^a^b = b^a^a = b实现
1
2
3
4
5
6
7int singleNumber(vector<int>& nums){
int res = 0;
for (auto i: nums)
res ^= i;
return res;
}
关键: XOR行为
#1122 Relative Sort Array
描述
1
2
3
4
5
6
7
8
9Given two arrays arr1 and arr2, the elements of arr2 are distinct,
and all elements in arr2 are also in arr1.
Sort the elements of arr1 such that the relative ordering of items in arr1
are the same as in arr2. Elements that don't appear in arr2
should be placed at the end of arr1 in ascending order.
Input: arr1 = [2,3,1,3,2,4,6,7,9,2,19], arr2 = [2,1,4,3,9,6]
Output: [2,2,2,1,4,3,3,9,6,7,19]思路
很直接,遍历arr2,对于arr2中所有元素,在arr1中找到这个元素,并且放到合适的位置,这个位置由变量index指示。看下图:
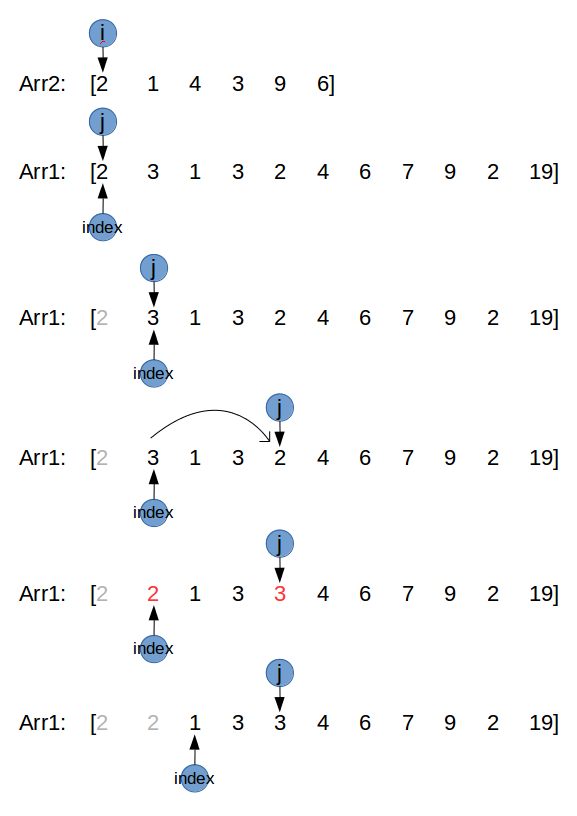
看图说话
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16vector<int> relativeSortArray(vector<int>& arr1, vector<int>& arr2){
int index = 0; // extra variable
for (int i=0; i<arr2.size(); i++){
for (int j=index; j<arr1.size(); j++){
if (arr1[j]==arr2[i]){
swap(arr1[j], arr1[index]);
index++;
}
}
}
sort(arr1.begin()+index, arr1.end());
return arr1;
}
关键: 额外变量的使用
#1009 Complement of Base 10 Integer
描述
1
2
3Input: 10
Output: 5
Explanation: 10 is "1010" in binary, with complement "0101" in binary, which is 5 in base-10.思路
找到对应的111…1,减去已知,得结果。
假设N=5,规律:binary dec 公式 判断 1 1 0*2+1 5>1 11 3 1*2+1 5>3 111 7 3*2+1 5<7 =>7-5=2 1111 15 7*1+1 11111 31 15*2+1
看图说话
1
2
3
4
5
6int bitwiseComplement(int N){
int x = 1;
while (N>x)
x = x*2+1;
return x-N;
}
关键:找到规律,数进制间的对应,
#868 Binay Gap
描述
1
2
3
4
5
6
7Input: 22
Output: 2
Explanation:
22 in binary is 0b10110.
1 <= N <= 10^9
其中相邻1与1之间距离最大的是2,所以返回2.思路
规律:一个整数的奇偶与其二进制的尾数相关,奇数对应位二进制的尾数是1;偶数对应二进制的尾数是0. 假如N=22:
N 左移一位结果 结果的二进制 与N的关系 22 10110 N左移0位 22>>1 11 01011 N左移1位 11>>1 5 00101 N左移2位 5>>1 2 00010 N左移3位 2>>1 1 00001 N左移4位 1>>1 0 00000 N左移5位
两方法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35///time: O(logN)
/// space: O(logN)
int binaryGap(int N){
vector<int> index;
int k=0;
int yu;
while (N!=0){
k++;
yu = N%2;
if (yu == 1)
index.push_back(k);
N/=2;
}
int res=0;
for (int i=0; i<index.size()-1; i++){
res = max(res, index[i+1]-index[i]);
}
return res;
}
///time: O(logN)
/// space: O(1)
int binaryGap(int N){
int last = -1, res=0;
for (int i=0; i<32; i++){
if (((N>>i)&1) > 0) {
if (last >= 0)
res = max(res, i-last);
last = i;
}
}
return res;
}
关键:移位操作,找到问题的等价信息
#985 Sum of Even Numbers After Queries
描述
1
2
3
4
5
6
7
8Input: A = [1,2,3,4], queries = [[1,0],[-3,1],[-4,0],[2,3]]
Output: [8,6,2,4]
Explanation:
At the beginning, the array is [1,2,3,4].
After adding 1 to A[0], the array is [2,2,3,4], and the sum of even values is 2 + 2 + 4 = 8.
After adding -3 to A[1], the array is [2,-1,3,4], and the sum of even values is 2 + 4 = 6.
After adding -4 to A[0], the array is [-2,-1,3,4], and the sum of even values is -2 + 4 = 2.
After adding 2 to A[3], the array is [-2,-1,3,6], and the sum of even values is -2 + 6 = 4.思路
第一步:原始A数组偶数求和sum
第二步:对于queries中的每个元素执行如下操作:
1. 如果A中待改变索引的数为even,则从sum中把这个索引对应的数减去。(因为不知道更新后的实际是偶) 2. 更新A数组。 3. 更新后的A中被修改的数如果是even,则把他加到sum中。(更新后的奇偶知道了) 4. 记录sum。实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16vector<int> sumEvenAfterQueries(vector<int>& A, vector<vector<int>>& queries) {
vector<int> res;
int sum = accumulate(A.begin(), A.end(), 0, [](int s, int a){
return s+(a%2==0?a:0);
});
for (auto q:queries){
if(A[q[1]]%2==0)
sum-=A[q[1]]; // 1.
A[q[1]] += q[0]; //2.
if (A[q[1]]%2==0)
sum+=A[q[1]]; //3.
res.push_back(sum); // 4.
}
return res;
}
关键:直接想到的方法通常不是最好的,lambda函数