#213 House Robber II
描述
1
与#198不同,这回抢的街是环形,即首位相连,依旧是在不相邻的房子间抢,求可获得的最好收益。
逻辑
技巧:选择一个房子作为首:第一条街偷除第一个房子的其他房子,第二次偷除最后一个房子的其他房子。两次偷的结果取较大值。
其中每次偷房子的方式同#198.实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35int rob(vector<int>& nums) {
if (nums.size() == 0) return 0;
if (nums.size() == 1) return nums[0];
if (nums.size() == 2) return max(nums[0], nums[1]);
// 最后一间房子 不强
vector<int> memo1(nums.size(), 0);
memo1[0] = nums[0];
memo1[1] = max(nums[0], nums[1]);
for (int i=2; i<nums.size(); i++){
int tmp=0;
for (int j=0; j<=i-2; j++)
if (memo1[j]>tmp)
tmp = memo1[j];
memo1[i] = max(memo1[i-1], nums[i]+tmp);
}
// 第一间房子 不强
vector<int> memo2(nums.size(), 0);
memo2[1] = nums[1];
memo2[2] = max(nums[1], nums[2]);
for (int i=3; i<nums.size(); i++){
int tmp=0;
for (int j=0; j<=i-2; j++)
if (memo2[j]>tmp)
tmp = memo2[j];
memo2[i] = max(memo2[i-1], nums[i]+tmp);
}
return max( memo1[nums.size()-2], memo2[nums.size()-1]);
}
#96Unique BST
描述
1
2
3给出一个正整数n,返回从1~n可以构成不同BST 的个数。
如n=3时,可以构成的BST数量为5.逻辑
动手找几个n值画画图,从中找规律。
状态的定义:
memo[i]表示以1~i为节点的 BST的个数。定义memo[0]=1.状态转移方程:看下示意图,以n=3为例:
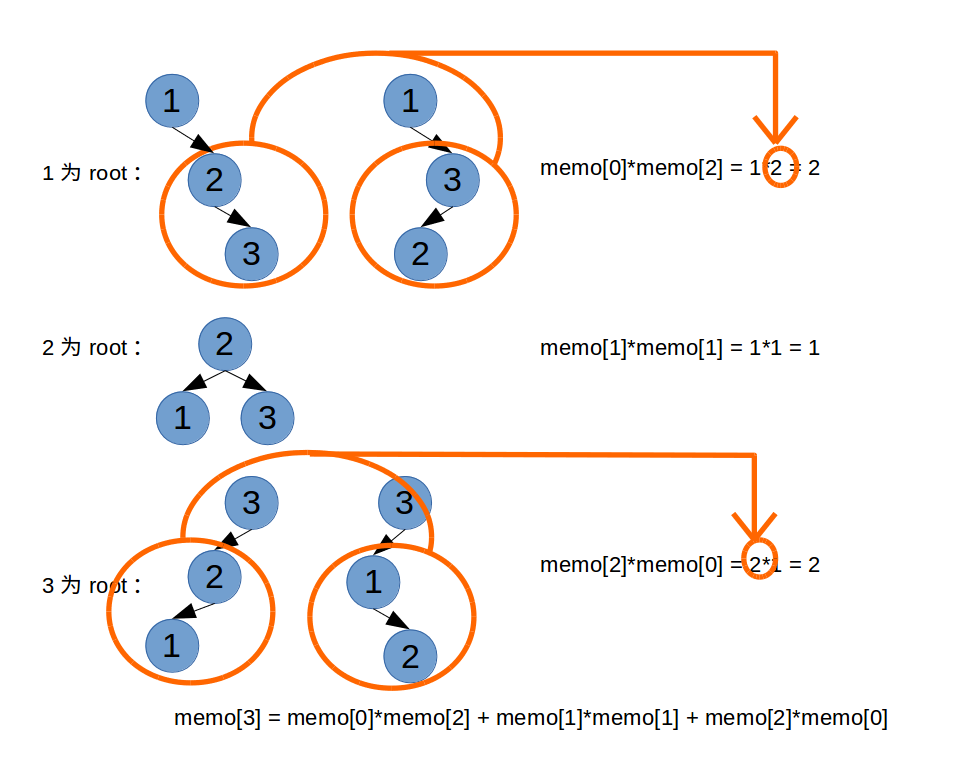
图中
memo[3]=memo[0]*memo[2] + memo[1]*memo[1] + memo[2]*memo[0]就是n=3时的状态转移方程。这其中
memo[2]=memo[0]*memo[1] + memo[1]*memo[0]=2是n=2时的状态转移方程。当n=4:
memo[0]=1;
memo[1]=memo[0]*memo[0]=1;
memo[2]=memo[0]*memo[1] + memo[1]*memo[0]=2;
memo[3]=memo[0]*memo[2] + memo[1]*memo[1] + memo[2]*memo[0]=5;
memo[4]=memo[0]*memo[3] + memo[1]*memo[2] + memo[2]*memo[1] + memo[3]*memo[0]=14;可以观察出,要想求出
memo[1],需要求出memo[0],要想求出memo[2],需要求出memo[1]和memo[0]...。
实现
1
2
3
4
5
6
7
8
9
10int numTree(int n){
vector<int> memo(n+1, 0);
memo[0] = 1;
for (int i=1; i<=n ;i++){
for (int k=1; k<=i; k++){
memo[i] += memo[k-1] * memo[i-1-(k-1)];
}
}
return memo[n];
}
关键:找规律,
#304 Sum of Region
描述
1
2
3
4给定一个矩阵,和两个点, 左上角(r1,c1)和右下角(r2,c2)。
求出由这两个点围成的矩阵所有元素之和。
NOTE,对于同一个矩阵,需要大量的上述query操作。逻辑
第一步:构建memo
状态定义:
memo[i][j]表示从matrix最左上角到matrix[i][j]处的元素之和。状态转移方程 看下图示,假如matrix如作图所示:
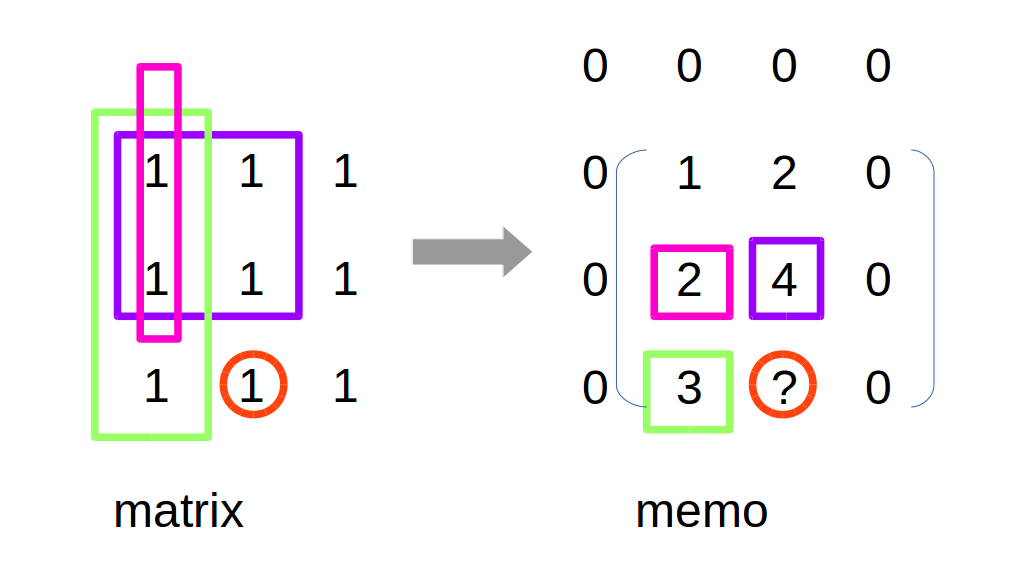
memo中的红圈重点值如何得到? 红圈中的值按照定义,等于matrix最左上角到红圈的元素和,从作图中看就是6,怎么算的?
6=绿+紫-粉+自身。在右图中就等于绿+紫-粉+1=6。所以状态转移方程是:
当前memo值=左边memo值+上边memo值+当前matrix值-左上memo值。在实现中, 由于要对memo第一行和memo第一列做同样的操作,所以memo大小较matrix多了一行一列。
第二步:query 从memo中取所需值。
过程如下图:注意根据memo的定义,在matrix中的矩形,一定是从matrix最左上角开始。
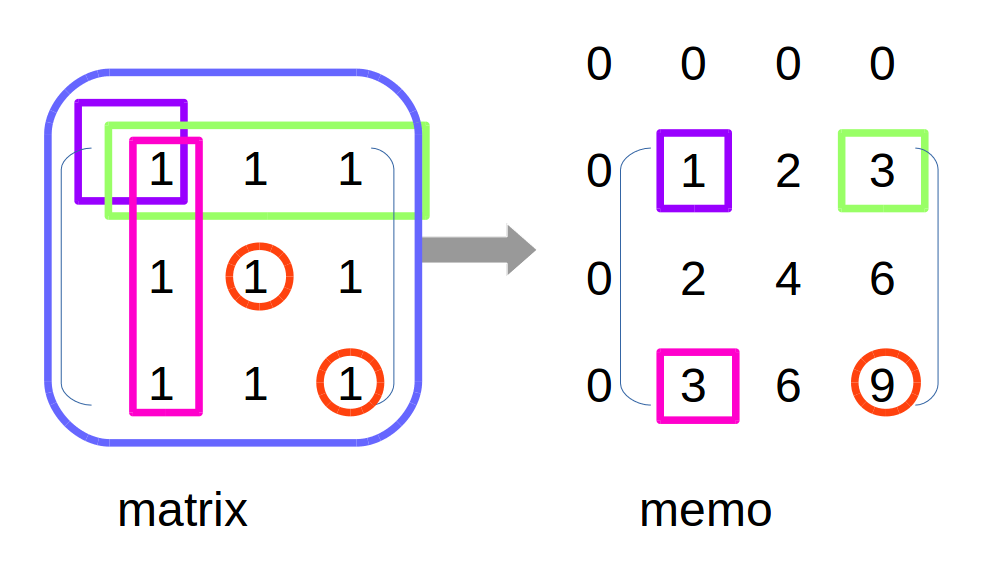
如上图所示,假如要得到matrix中
(1,1)到(2,2)元素和,在左边matrix矩阵中,就等于蓝-粉-绿+紫,对应于有图memo中就是红-粉-绿+紫。就是最终返回值。
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class NumMatrix{
private:
vector<vector<int>> memo;
public:
// 构建memo数组
NumMatrix(vector<vector<int>>& matrix) {
if (matrix.size()==0 || matrix[0].size()==0) return;
// 在原先matrix大小基础上增加一行一列,并且初始化为0
memo = vector<vector<int>>(matrix.size()+1, vector<int>(matrix[0].size()+1, 0));
for (int r=0; r<matrix.size(); r++){
for (int c=0; c<matrix[0].size(); c++){
// 状态转移方程:
memo[r+1][c+1] = memo[r][c+1] + memo[r+1][c] + matrix[r][c]-memo[r][c];
}
}
}
// 使用memo求出制定区域的元素之和。
int sumRegion(int row1, int col1, int row2, int col2) {
return memo[row2+1][col2+1]-memo[row1][col2+1]-memo[row2+1][col1]+memo[row1][col1];
}
};
关键:找规律
#70 Climb Staires
描述
1
你爬楼梯,每次只能爬1阶或2阶,那么要爬到n阶,由多少种走法
逻辑
逻辑与斐波那契数列相同。以n=5为例。
状态定义:memo[i]表示爬i阶台阶由多少中爬法。其中定义memo[0]=1, memo[1]=1。
状态转移方程:见下图:
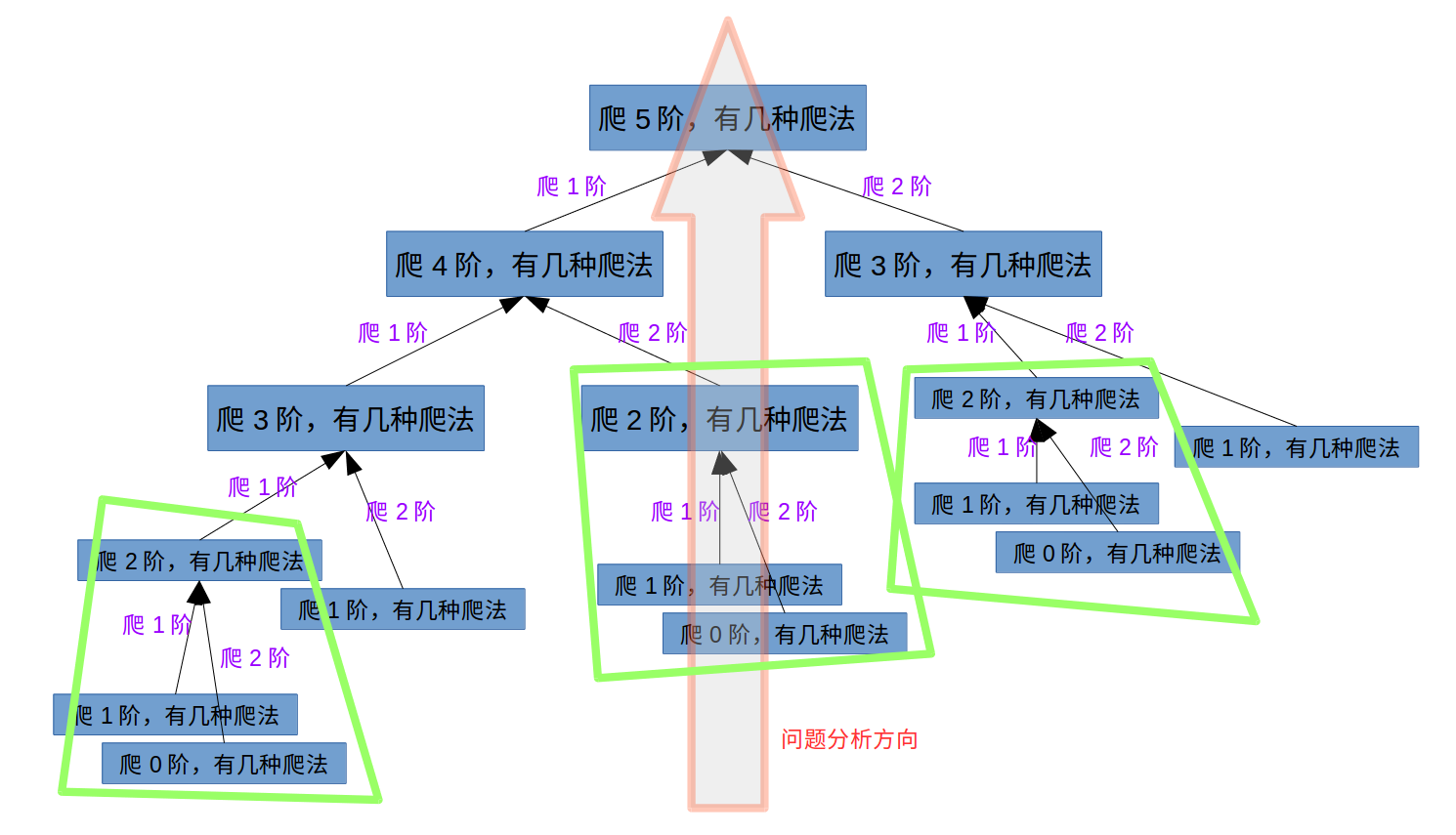
DP的特点是从已知计算求下一步结果,进而再求下下步结果。计算是由一个特定方向的。所以按照图中箭头方向分析:
爬2阶的爬法 = 爬1阶的爬法(爬了1阶,再爬1阶) + 爬0阶的爬法(爬了0阶,再爬2阶);爬3阶的爬法 = 爬2阶的爬法(爬了2阶,再爬1阶) + 爬1阶的爬法(爬了1阶,再爬2阶);爬4阶的爬法 = 爬3阶的爬法(爬了3阶,再爬1阶) + 爬2阶的爬法(爬了2阶,再爬2阶);...这一类问题有重复计算的子问题。所以DP的记忆化机制保存了中间的结果,从而避免了重复的计算。
实现
1
2
3
4
5
6
7
8
9
10int climbStairs (int numStairs) {
vector<int> memo(numStairs + 1, -1);
memo[0] = 1;
memo[1] = 1;
for (int i =2; i <= numStairs; i++) {
memo[i] = memo[i-1] + memo[i-2];
}
return memo[numStairs];
}