记录两种看待矩阵的重要视角,对于推理, 证明和理解线性代数其他概念都十分重要。
- 列向量 坐标系或空间
- 行向量 函数或线性方程组
列视角
两矩阵相乘,将左边的方阵A看做是坐标系或空间,右边的矩阵B是一个列向量的集合,每一个列向量表示在空间A的表式,而相乘的结果是在这个维度的空间中的标准正交基下的同一个列向量的表示。如
看个例子:
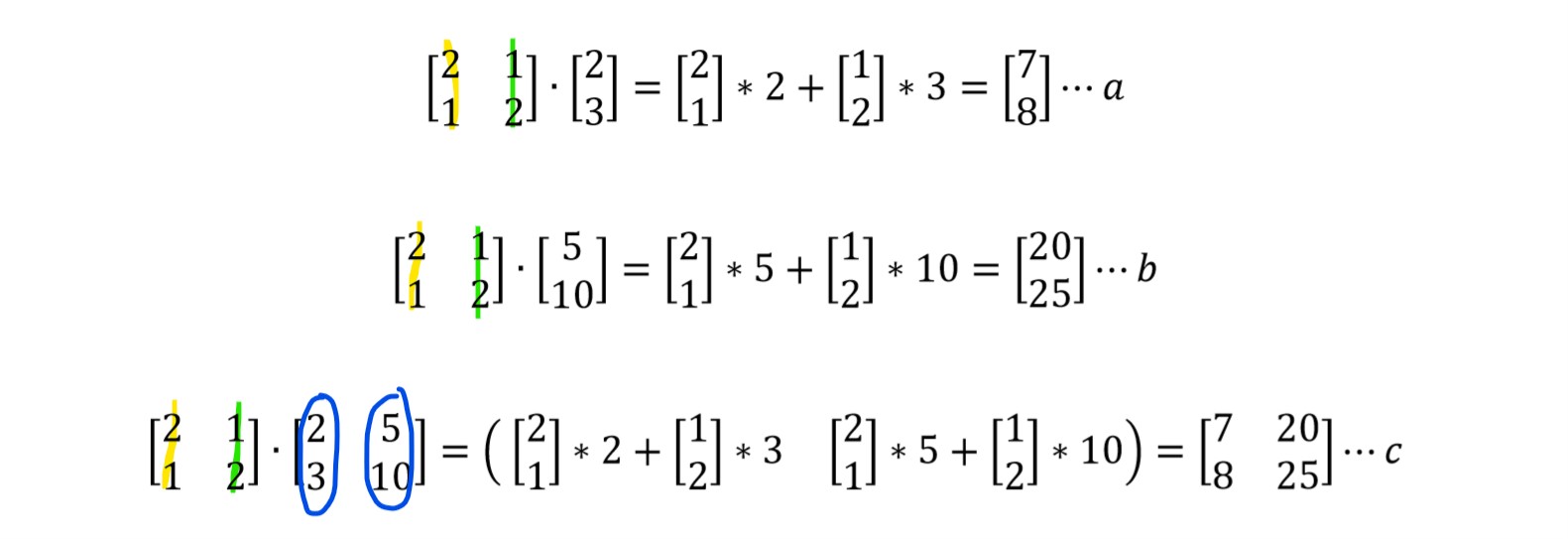
把矩阵A看做是由列向量构成的,a,b 是两个列向量经过A变换得到的结果。c 是将两个列向量放在一起,构成了矩阵B,矩阵B中每个列向量经过A变换的结果。
结果是相同的。向量trans([2,3]) 是向量trans([7,7])在空间A中的表达,
行视角
还可以将A看作是一个函数或线性方程组. 右边的向量或矩阵是操作对象。
看个例子:
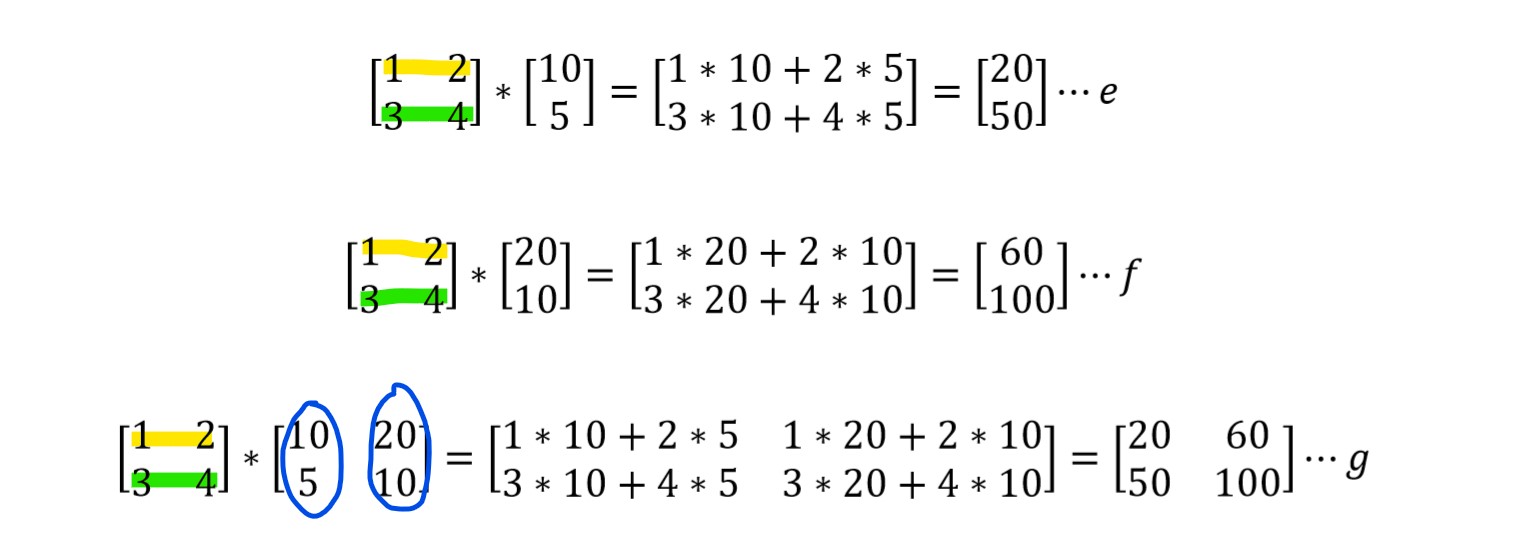
把矩阵A看做是由行向量构成,e,f 是分别操作两个列向量。g 是将两个列向量放到一起,一起处理。
结果相同,可以看出B中的列向量彼此间是无关的,都经过A相同的变换。
一个例子
证明矩阵对角化中一个结论:
如果可以将A分解成P*D*(P逆). 那么有D和P可以分别为:
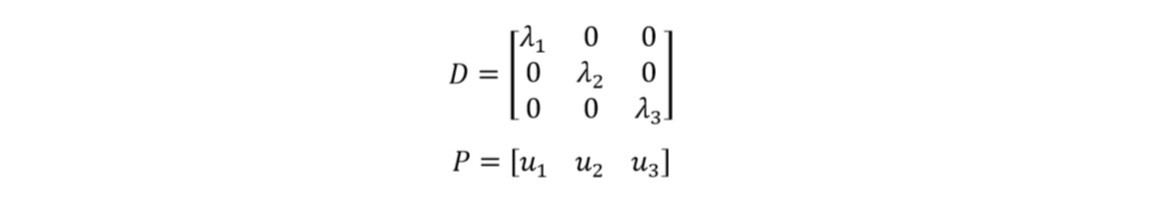
其中lambda为A所对应的所有特征值,u是对应lambda的特征向量。(P 中的u向量竖着写)。
现在问题是,如何证明:如果D,P为上述矩阵,A有n个线性无关的特征向量,那么有:
证明A=P*D*(P逆), 就是证明AP=PD,观察等号左右:
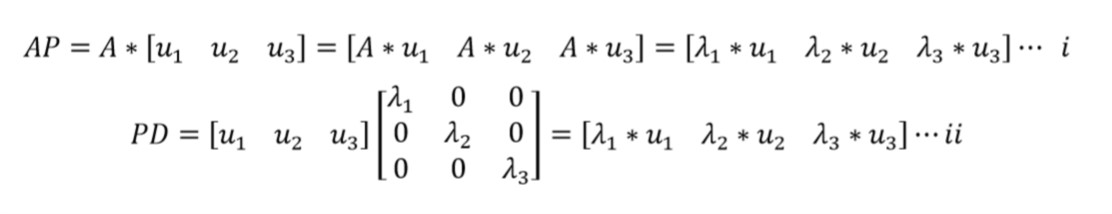
左右相等,证毕。
表达式i中A为一个函数,操作与右边每一个列向量。但并没有展开,因为根据特征值特征向量的定义,可以将A用lambda替换。
而表达式ii的过程,就是将左边矩阵每一列当成一个列向量考虑,实际上,这个矩阵就是由列向量构成,所以自然而然的将这个矩阵用类向量的视角看待。