CUDA

CUDA-例-矩阵相乘

矩阵相乘CPU版本

思路：三重循环，

  • 外层：遍历结果矩阵所有行，
  • 中层：对结果矩阵每一行，遍历所有列，
  • 内层：结果矩阵某一行某一列元素的得到，需要A矩阵对应行，B矩阵对应列，的元素相乘后累加，这需要一个循环。内层循环结束后，就得到结果矩阵中的一个元素。

看图：

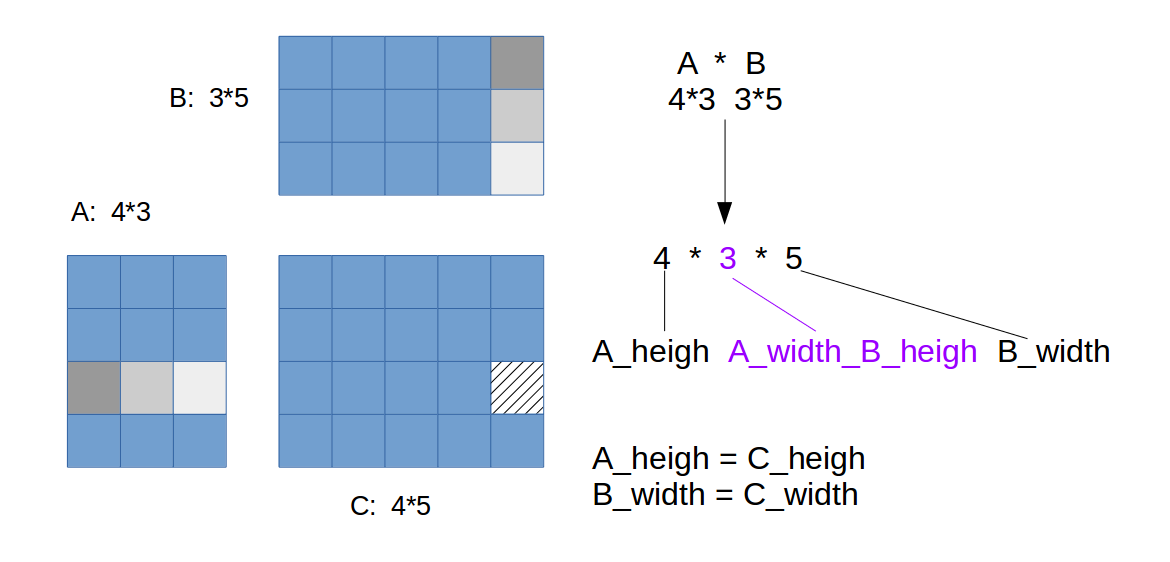
实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void matrixMultiplicationCPU(float* M, float* N, float* P, 
                                int A_height, int Awidth_Bheight, int B_width){

    for (int i=0; i < A_height; i++){
        for (int j=0; j < B_width; j++){
            float sum = 0;
            for (int k=0; k < Awidth_Bheight; k++){
                float a = M[i * Awidth_Bheight + k];
                float b = N[k * B_width + j];
                sum += a * b;
            }
            P[i * B_width + j] = sum;  
        }
    }
}

其中，M的大小为（A_height x Awidth_Bheight），N的大小为（Awidth_Bheight x B_width）. 注意中括号内，索引的计算。

未优化的矩阵相乘kernel

参数：

  • AColBRow：AxB中A的列数，也是B的行数
  • BCol：B的列数
  • a，b矩阵的元素索引按行标注索引
1
2
3
4
5
6
7
8
9
10
__global__ void simpleMultiply2(float *a, float* b, float *c){

    int row = threadIdx.y;
    int col = threadIdx.x;
    float sum = 0.0f;
    for (int i = 0; i < AColBRow; i++) {
        sum += a[row * AColBRow + i] * b[i * BCol + col];
    }
    c[row * BCol + col] = sum;
}

这种方法中每一个线程负责乘累加结果的一个元素，这个元素的得到是通过循环读取a矩阵的一行，b矩阵的一列，后乘累加得到。这个过程其实就是把CPU版本中的外循环和中层循环去掉，替代这两个循环的是threadIdx.x和threadIdx.y，这两个值自加。对于a和b的访存索引的计算是不变的。因为不涉及到结果间的依赖，所以不需要同步机制。

缺点：

  • 观察row和col的定义，发现这个实现只使用了一个block。对于大的矩阵相乘，一个block不足以覆盖所有元素。
  • 矩阵相乘的过程中，同一个Global memory地址被频繁访问，所以速度慢。

多blocks分块处理矩阵相乘

参数：

  • AColBRow：AxB中A的列数，也是B的行数
  • BCol：B的列数
  • a，b矩阵的元素索引按行标注索引
1
2
3
4
5
6
7
8
9
10
__global__ void simpleMultiply2(float *a, float* b, float *c){

    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;
    float sum = 0.0f;
    for (int i = 0; i < AColBRow; i++) {
        sum += a[row * AColBRow + i] * b[i * BCol + col];
    }
    c[row * BCol + col] = sum;
}

此情况的线程结构是2D block，2D thread，注意线程组织的index，事实上是这样的：

注意：横向，index的第一个分量递增；纵向，index的第二个分量递增。

与上一种方法相比，优势是，使用多个blocks，每个block负责结果矩阵中的一个矩形块中的元素。
每个thread的操作细节看下图：

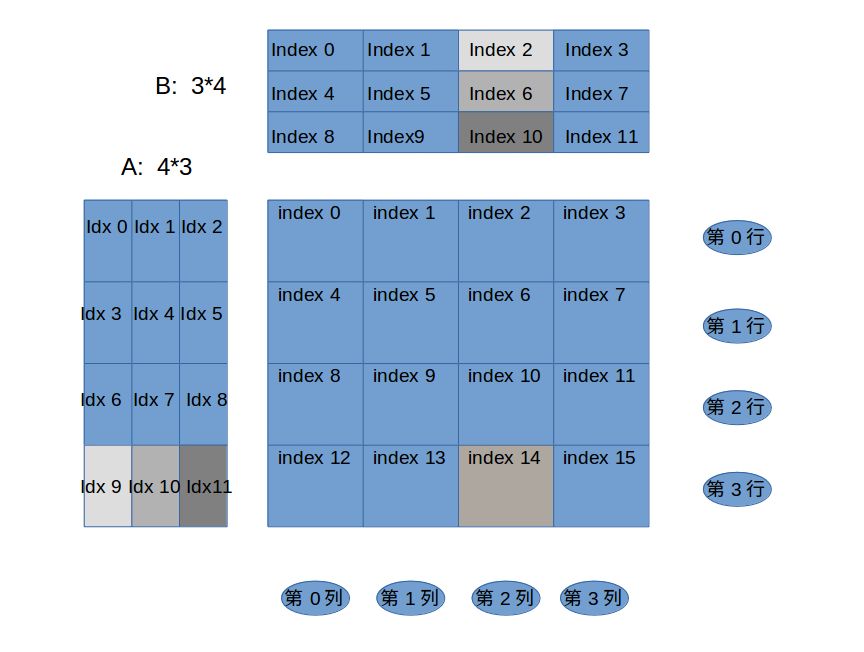
注意，C/C++中矩阵元素是按行排列的。假设线程组织是2D thread 2D block，假设tile大小是2x2的，假设使用4个blocks。那么跟踪上述code可得到结果矩阵中的第14个元素：

1
2
3
4
5
6
7
row = 3;
col = 2;
i=0: a[row * 3 + i] * b[i * 4 + col] = a[9] *b[2];
i=1: a[row * 3 + i] * b[i * 4 + col] = a[10]*b[6];
i=2: a[row * 3 + i] * b[i * 4 + col] = a[11]*b[10];
GET sum;
WRITE sum INTO c[row * 4 + col] = c[14];

看出逻辑及结果是正确的。

有了kernel，如何调用kernel：

1
2
3
4
5
// block的个数
dim3 grid((A的行数+1)/tile的行数，(B的列数+1)/tile的列数)
// 每个block中的线程数
dim3 block(tile的行数，tile的列数)
simpleMultiply2<<<grid, block>>>(a, b, c)

比如图中

  • 定义tileRow=2，tileCol=2.
  • A的行数为ARow=4，列数ACol=3；
  • B的行数为BRow=3，列数BCol=4；

那么，有如下对kernel的配置，自然地每个tile的大小为2x2，每个block大的大小也是2x2. block与block之间相互不影响，所以所有blocks并行执行。

1
2
3
4
5
// block的个数，共有4个
dim3 grid(2，2)
// 每个block中的线程数，有4个
dim3 block(2，2)
simpleMultiply2<<<grid, block>>>(a, b, c)

其中tile是一个block处理区域的大小，也就是一个block的大小，比如2x2，3x4. 是开发者根据问题情况自己定义的（通常是32 的倍数）。通过结果矩阵的行列数和tile的行列数，可以计算出，所需block数量个blocks阵大小。

总结：这个优化算然可以处理任何大小的矩阵相乘，但是对global memory的读写并没有做优化。

Global memory慢

假如一个GPU的性能峰值时346.5 Gflops。所以需要346.5x4bit=1386 GB/s的带宽才能达到峰值。但是这个GPU的存储实际带宽可能只有86.4GB/s，也就是86.4GB/s / 4bit=21.6 Gflops的性能。而实际上代码运行的速度可能只有15 Gflops。只有峰值的1/20. 所以要尽量减少对global memory的访存。

对于矩阵相乘，可以使用shared memory来减少对global memory的访存。始终要有这个意识。

优化实列：使用shared memory优化矩阵相乘

Shared memory这么使用：

思路：

因为使用了若干个block来分块结果矩阵，每一个block有自己单独的shared memory，这个存储空间由这个block内的所有threads共享，而且就矩阵相乘这个问题，A矩阵的每一行，和B矩阵的每一列在计算这个块时会不止一次被使用。所以：

  • 将结果阵中这一块对应的A中行和B中列存入这个block对应的shared memory中，如此避免了对global memory的频繁访问。如下图：
  • 进一步，由于A和B会很大，存入shared memory中的A行，和B列也是分段的，避免了shared memory不够用。如下图：

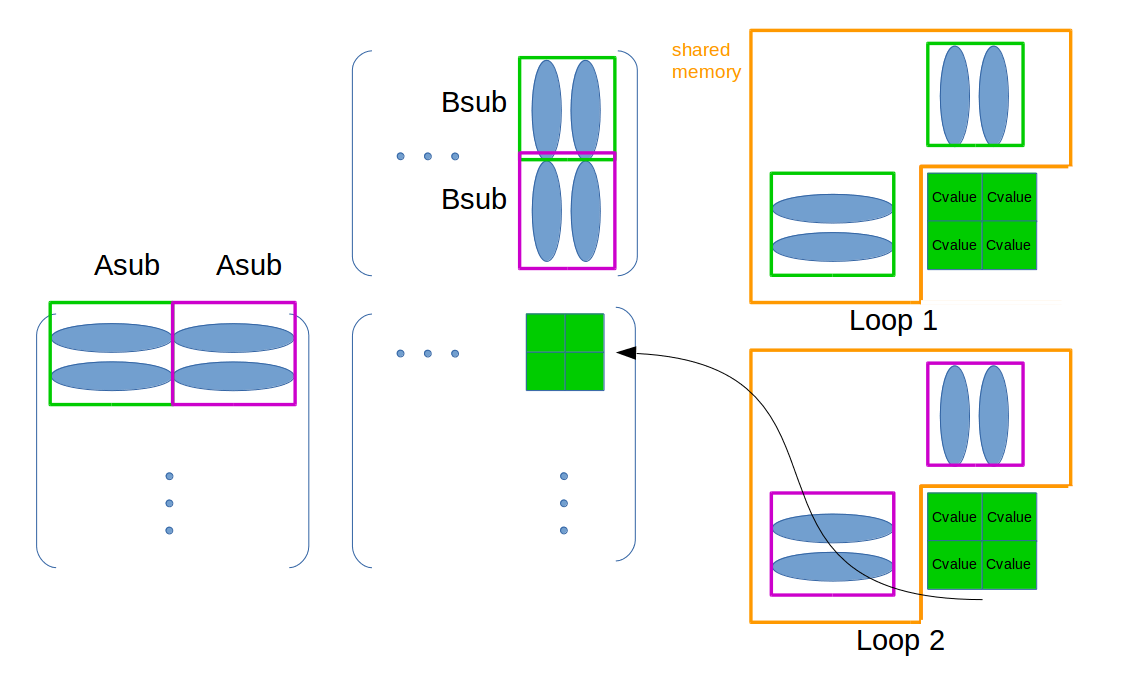
其中橘色是这个block的Shared memory空间，循环所有的Asub和Bsub，先绿色后紫色，将每次的元素放入Shared memory，求得结果累加到Cvalue。循环结束后将最终的Cvalue写入最终位置，见图中箭头，

kernel函数包含二重循环：

  • 外层，循环所有的Asub和Bsub，并将其放入Shared memory中。
  • 内层，循环求Asub每部分行和Bsub每部分列的部分乘累加和Cvalue。

Bare in mind，每一个thread处理一个结果阵中的一个元素，也就是说，kernel函数是一个thread得到一个结果矩阵中的一个元素。

官方文档中有官方的解释，可以参考。

注意，整个过程中有两处同步操作，因为涉及到线程间的同步。

程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
__global__ void MatMulKernel(Matrix A, Matrix B, Matrix C)
{
    // block的行ID和列ID
    int blockRow = blockIdx.y;
    int blockCol = blockIdx.x;

    // 每个block计算结果矩阵中的一块
    Matrix Csub = GetSubMatrix(C, blockRow, blockCol);

    // 每个thread计算结果矩阵中的一个元素，
    // 这个结果通过累加存入Cvalue
    float Cvalue = 0;

    // thread的行ID和列ID
    int row = threadIdx.y;
    int col = threadIdx.x;

    // Loop over all the sub-matrices of A and B that are
    // required to compute Csub
    // Multiply each pair of sub-matrices together
    // and accumulate the results to Cvalue
    for (int m = 0; m < (A.width / BLOCK_SIZE); ++m) {

        // 得到这个block在这次循环中的A的子矩阵
        Matrix Asub = GetSubMatrix(A, blockRow, m);

        // 得到这个block在这次循环中的B的子矩阵
        Matrix Bsub = GetSubMatrix(B, m, blockCol);

        // 保存A的子矩阵和B的子矩阵
        __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
        __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];

        // Load Asub and Bsub from device memory to shared memory
        // 每个thread加载A的子矩阵中一个元素，和B的子矩阵中的一个元素
        As[row][col] = GetElement(Asub, row, col);
        Bs[row][col] = GetElement(Bsub, row, col);

        // 将A中这部分所有的元素，和B中元素都写入到shared memory中后，
        // 才能开始下面的操作。
        __syncthreads();  

        // 计算当前A的子矩阵与B的子矩阵，相乘后累加结果。
        // 当外层循环结束，表示累加每一块累加的结果完成，
        // 得到最后的C中这个位置的结果。
        for (int e = 0; e < BLOCK_SIZE; ++e)
            Cvalue += As[row][e] * Bs[e][col];

        // Synchronize to make sure that the preceding
        // computation is done before loading two new
        // sub-matrices of A and B in the next iteration
        // 等待这一阶段的 加类乘完成后，才能够进行下一次循环，更新shared memory中的内容。
        __syncthreads();
    }

    // Write Csub to device memory
    // Each thread writes one element
    SetElement(Csub, row, col, Cvalue);
}

那么对global memory 的访问减少了多少倍呢?

  • 假如一个block计算2x2的结果C的子矩阵，那么未优化的实现要访问Global memory (2*2*2)8次行/列（定义1次行/列：访问A的完整一行或B的完整一列）。优化后只访问4次行/列。8/4=2，就是tile的宽。
  • 假如一个block计算3x3的结果C的子矩阵，那么未优化的实现要访问Global memory (2*3*3)18次行/列。优化后只访问6次行/列。18/6=3，就是tile的宽。
  • 假如一个block计算100x100的结果C的子矩阵，那么未优化的实现要访问Global memory (2*100*100)20,000次行/列。优化后只访问200次行/列。20,000/200=100，就是tile的宽。

所以对于很大的矩阵，优化前后的性能差别是巨大的。相差tile宽，这么多倍。

相差tile宽，这么多倍。极限情况下，如果shared memory有足够的空间，可以把A，B都放入每个block的shared memory中。此情况下对global memory的访问最少。

上述优化方法中确定块tile的宽度要考虑shared memory的大小：

尽量最大化tile，block的大小

假如一个GPU每个SM有16kB的shared memory，并且每个SM有8个blocks。可以算出每个block可以使用2kB的shared memory。

其中1kB存矩阵A的相关元素，1kB存B的相关元素。假设数据类型是float，占4B。所以可以计算出1kB=16x16x4。block的大小为16x16. 也就是一个block有16x16个threads。

这种情况充分使用了SM的threads和shared memory资源，最大化资源占用率。