CUDA

CUDA-例-规约

优化实列：并行规约（parallel reduction）

规约的更为一般的形式：对一个输入数组进行某种操作，会产生一个更小的结果数组。比如点积算子，累加，min，max，平方和，逻辑与，逻辑或等等。规约的成立前提是，这些算子中的二元操作符合结合率。

未优化的规约（为便于图中展示，假设warp大小为2）

过程看图：

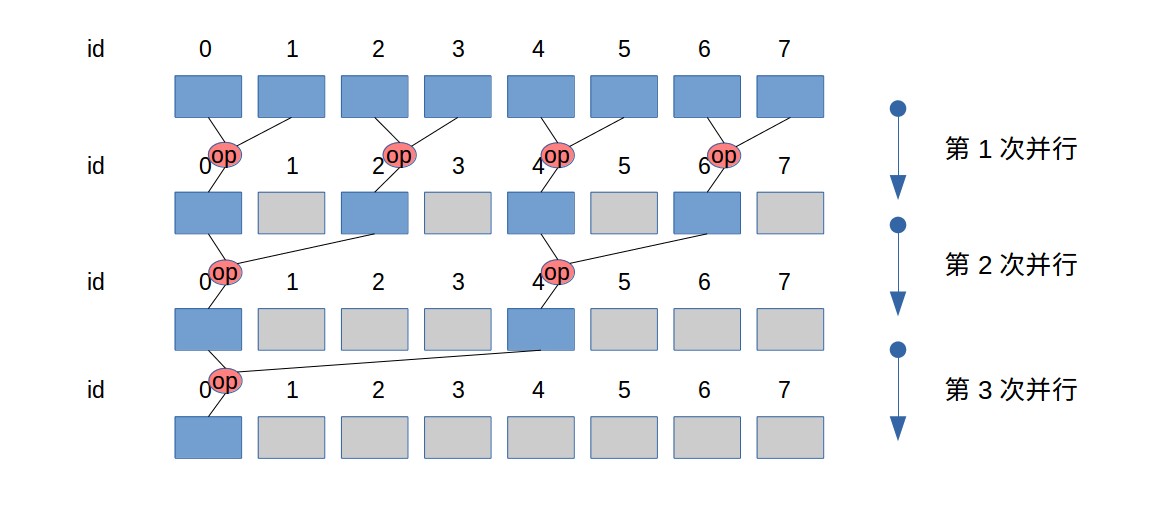
其中

  • id既是存储地址的id，也是threads的id。（因为threads的id此处没有更新）。
  • n个元素需要lg(n)次平行。
  • 上图从上到下，是在时间上展开，并没有新的空间被使用。

warp大小为2，从一开始的第一次并行，就存在divergence。

过程实现（假如在shared memory中实现）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
__global__ void func(){

    __shared__ float partialSum[];
    // ...将数据放入shared memory中

    // 因为只使用一个block，所以只需要threads 的id
    int x = threadIdx.x;

    // 循环计算每一层，stride 为 1，2，4
    for(int stride=1; stride < blockDim.x; stride *= 2){
        // 对指定的thread 进行加操作，与id和stride有关，拿笔画画就找到规律。
        if (x % (2*stride) == 0)
            partialSum[x] += partialSum[x + stride];

        // 这一层都求和结束后，才能进行下一步
        __syncthreads();
    }
}

上述过程中，（看图）每次循环会规律的有线程没有做实际的工作，这些threads也在工作（因为是在同一个warp中），但是没有实际操作数。每一轮实际所需的线程数在减半。

优化后规约（为便于图中展示，假设warp大小为2）

由上一个实现中，看到了，每一轮的实际工作线程数在减半，但是实际上所有的threads都在工作，很多是没有意义的工作。

这样为什么不好？因为违反了Coalescing Access：相邻的线程处理相邻位置的数据.

所以改进如图：

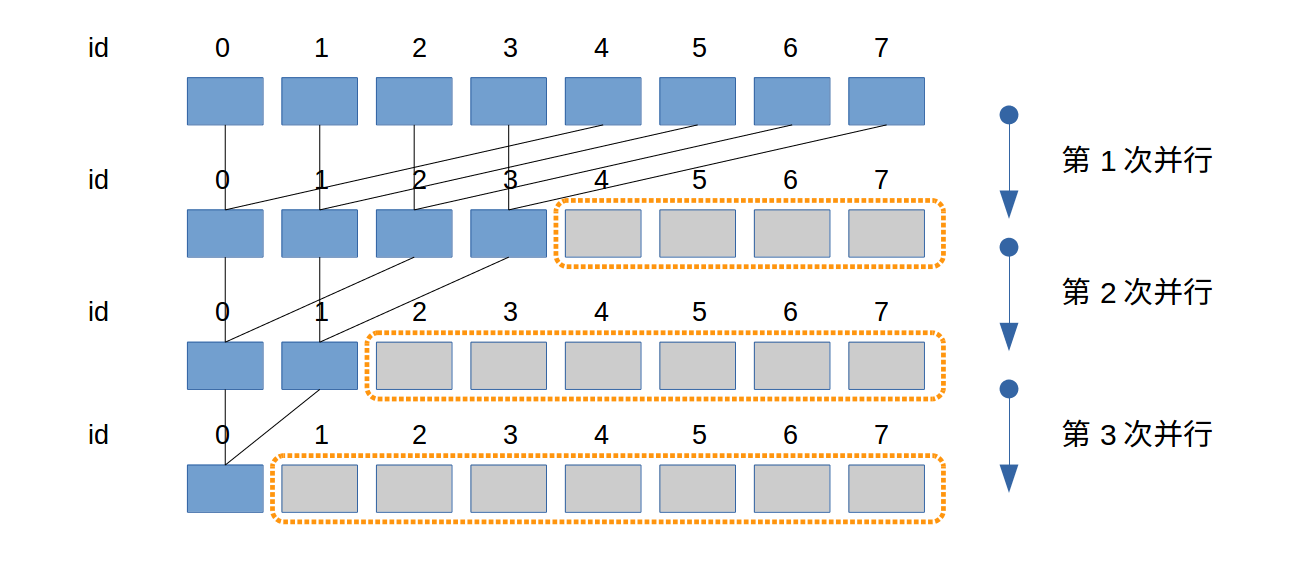
其中：

  • id既是存储地址的id，也是threads的id。（因为threads的id此处没有更新）。
  • n个元素需要lg(n)次平行。
  • 当数据元素更多时，橙色虚线框对应的threads与其他threads（很多时候）不属于同个warp，所以threads所用资源较前一个实现提前释放。

warp大小为2，图中所有次并行计算都不存在divergence。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
__global__ void func(){

    __shared__ float partialSum[];
    // ...将数据放入shared memory中

    // 因为只是用一个block，所以只需要threads 的id
    int x = threadIdx.x;

    // 循环计算每一层，stride 为 4，2，1
    for(int stride=blockDim.x/2; stride > 0; stride /= 2){
        // 对特定的thread 进行加操作，与id和stride有关，拿笔画画就找到规律。
        if (x < stride)
            partialSum[x] += partialSum[x + stride];

        // 这一层都求和结束后，才能进行下一步
        __syncthreads();
    }
}

为什么此法好？

  1. 每一轮都有一半的 thread不需要工作，资源释放掉。让warp提前完工，释放资源。
  2. block中的warp，没有了分支发散，或者说是最小化了分支发散。回忆warp：
    • 在一个block中，连续的32个threads一组构成一个warp;
    • warp 是最基本的调度单元
    • warp中的threads在同步执行相同的指令（SIMT）
    • warp中threads需要执行不同 的路径时（分支发散），warp中每个threads都要执行所有的分支，因为是同步的。比如一个宿舍的6个学生可以是一个warp，今天有的想先上厕所，后吃饭，而有的不需要上厕所，此时所有的同学都会一起先上厕所，后一起吃饭。
    • warp之间是没有关系的。
    • warp间的切换时没有代价的。多warp工作可以隐藏延时
    • warp的分割，连续32个threadIdx.x 为一组（一个warp）0到31，32到63，…
    • warp中的分支发散不总是问题，但是如有很多分支语句的话，每个thread就需要执行所有的分支。
    • 在设计程序时，不应个这样：if (threadIdx.x > 15){...} 而应该这样if (threadIdx.x > 32-1) {...}。后者，表示说，第一个warp干他的事，第二个warp执行这个分支。

就这个优化，当元素的个数小于32（warp的大小）时，不可避免的会产生分支发散。