2020-02-20

CUDA

CUDA-再看规约-循环展开

循环展开

循环展开减少了循环中的变量的判断，自加等其他操作，是提升性能一个手段。

1
2
3

for (int i=0; i<1000; i++){
    a[i] = b[i] + c[i];
}

将循环次数减少一半：

for (int i=0; i<1000; i+=2){
    a[i] = b[i] + c[i];
    a[i+1] = b[i+1] + c[i+1];
}

下面的两段规约法，展示使用完全的循环展开。

再看规约-两段规约

类似与点积中的两段法。两段规约同样使用shared memory。

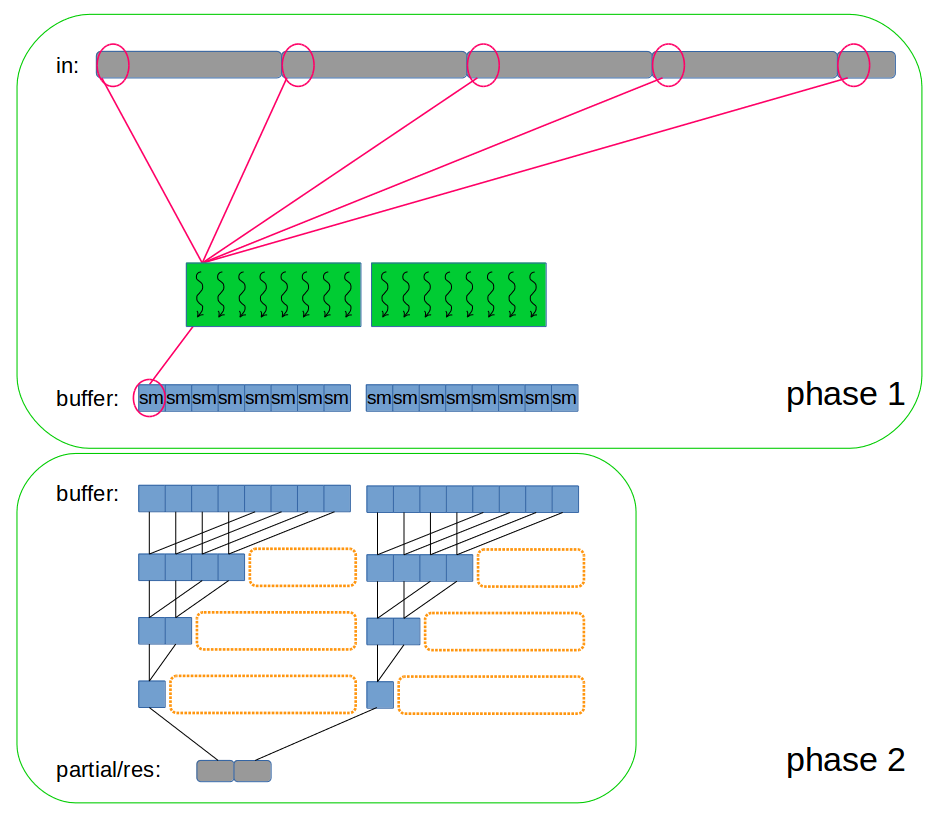
过程见下图：

实现上图过程：

/*
* in: 待读取的数组。out: 待写入的数组。N: in数组的长度
*/
__global__ void reductionKernel(int* out, int* in, size_t N){
    // 此处是一个未分配大小的shared memory
    __shared__ int buffer[];

    // 第一阶段，
    int sum=0;
    int tid = threadIdx.x + blockDim.x * blockIdx.x;
    int stride = blockDim.x * gridDim.x;
    // 使用stride loop
    for (size_t i = tid; i<N; i+=stride){
        sum += in[i];
    }
    buffer[threadIdx.x] = sum;
    // 等待得到所有threads的sum值
    // block与block之间怎样同步呢？这里不需要同步
    __syncthreads();   

    // 第二阶段，规约求每个block的最终值
    for (int i = blockDim.x >> 1; i!=0; i>>=1){
        if (threadIdx.x < i){
            buffer[threadIdx.x] += buffer[threadIdx.x + i];
        }
        __syncthreads();
    }
    // 最后一步，将每个block对应的buffer中的第一个元素放入out数组
    // 此时out数组中存放的是每个block的最终值。
    if (threadIdx.x == 0)
        out[blockIdx.x] = buffer[0];
}

分析说明：

强调：第一阶段的blockDim.x应该是32的倍数，每个block对应的Shared memory大小也要是32的倍数。这样才能保证在第二阶段所处理的数据是整齐的。
第二阶段结束后block与block间结果怎样同步？kernel函数执行完毕，表示两个block都得到了结果，即同步了。所以一种方式的到最终结果是两次调用这个kernel函数。见下面code。
对out数组的最终处理，可以考虑将out传回host后在CPU中计算，就像向量点积。也可以使用一个block，第二次调用上述kernel函数，得到最终值。（我感觉不如传回CPU）。
shared memory 的访问索引是threadIdx.x。因为一个block共用一段Shared memory，所以Shared memory的不同地址可用这个block的threadIdx.x唯一标识。
使用blockDim.x >> 1和i>>=1，这属于指令优化。
kernel中的Shared memory可以不分配大小，调用kernel函数时再指定大小。

在Host中调用kernel函数：

void reduction(int* res, int* partial, int* in, 
                size_t N, int numBlocks, int numThreads){
    int sharedSize = numThreads*sizeof(int);
    // 第一个kernel得到所有block对应的buffer，
    // 这些block之间没有同步，所以只有所有的block的buffer都得到了
    // 这个kernel才时执行结束，也就是说，为了同步所有的block的buffer，
    // 只能再调用一次这个和函数了。
    reductionKernel<<<numBlocks, numThreads, sharedSize>>>
                    (partial, in, N);
    reductionKernel<<<1, numThreads, sharedSize>>>
                    (res, partial, numBlocks);
}

看到了吧：

block间的同步，其实是当该kernel函数执行结束后，自动同步。
第二次调用相同的kernel，只使一个block。
注意：此处在<< , , >>>中出现了第三个参数，由于在kernel中，没有指定shared memory的大小，所以在调用kernel函数时要制定大小了。
这个kernel中的第二个for循环中，循环的之后阶段，当threads数小于等于32时，可以特殊处理，此时的所有活动threads在一个warp中，所以不需要同步。细节间32特殊处理规约。
补充：每个block中的warp时按照lockstep的方式执行每条指令。

再看规约-第二阶段循环展开

优化意识：当threads数小于等于32时，也就是threadIdx.x从0到31时，可以特殊处理。这种处理就是循环展开。

/*
* in: 待读取的数组。out: 待写入的数组。N: in数组的长度
*/
__global__ void reductionKernel(int* out, int* in, size_t N){
    // 此处是一个未分配大小的shared memory
    __shared__ int buffer[];

    // 第一阶段，
    int sum=0;
    int tid = threadIdx.x + blockDim.x * blockIdx.x;
    int stride = blockDim.x * gridDim.x;
    // 使用stride loop
    for (size_t i = tid; i<N; i+=stride){
        sum += in[i];
    }
    buffer[threadIdx.x] = sum;
    // 等待得到所有threads的sum值
    __syncthreads();

    // 第二阶段，规约求每个block的最终值, 直到i=32.
    // 之后就是特殊处理了
    for (int i = blockDim.x >> 1; i>32; i>>=1){
        if (threadIdx.x < i){
            buffer[threadIdx.x] += buffer[threadIdx.x + i];
        }
        __syncthreads();
    }

    // 第三步，当元素个数小于等于32时：
    // 这个展开避免了循环控制的开销，和thread同步的逻辑
    if(threadIdx.x < 32){
        volatile int* wsSum = buffer;
        if(blockDim.x > 32)
            wsSum[threadIdx.x] += wsSum[threadIdx.x + 32];
        // 一下5条指令，一定都会被执行，不过也可以加上if条件。
        wsSum[threadIdx.x] += wsSum[threadIdx.x + 16];
        wsSum[threadIdx.x] += wsSum[threadIdx.x + 8];
        wsSum[threadIdx.x] += wsSum[threadIdx.x + 4];
        wsSum[threadIdx.x] += wsSum[threadIdx.x + 2];
        wsSum[threadIdx.x] += wsSum[threadIdx.x + 1];
        if (threadIdx.x == 0){
            volatile int* wsSum = buffer;
            out[blockIdx.x] = wsSum[0];
        }
    }
}

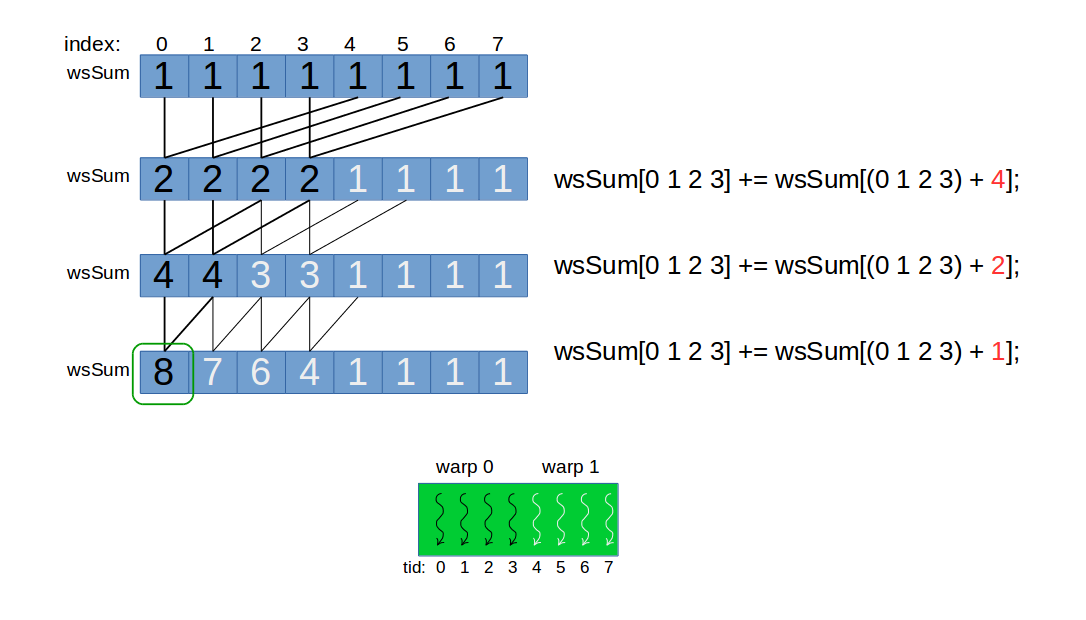
注意：当编写warp同步的code时，必须对shared memory 的指针使用volatile关键字。这个关键字告诉编译器必须将wsSum[threadIdx.x]的值存回global中。如果没有volatile，为什么不能得到正确结果？

第三步为什么正确，看下图之前，假设：

下图将大小为32的warp假设为4，即warp size=4：
所展示的情况是从上一个图片中的第一阶段的结果开始，即blockDim.x=8.

对于code中的第三步，见下图：

从上述code第二阶段的循环开始：

blockDim.x=8;
for(i=8>>1; i>4; i>>=1){
    i=4, i!>4, 退出循环;
}

对于 threadIdx.x<4，blockDim.x>4，即 0 1 2 3. 执行下面操作：
wsSum[0 1 2 3] += wsSum[(0 1 2 3) + 4];
wsSum[0 1 2 3] += wsSum[(0 1 2 3) + 2];
wsSum[0 1 2 3] += wsSum[(0 1 2 3) + 1];

说明：

其中执行单元只有这个block 中的第一个warp。
最终需要的是每个block对应buffer是第一个值，所以除第一个位置以外的位置，其值是无意义的。但是由于warp中的线程执行相同的指令，所以warp中其他threads也工作了，只不过这些结果我并不需要。
再强调：第一阶段的blockDim.x应该是32的倍数，每个block对应的Shared memory大小也要是32的倍数。这样才能保证在第二阶段所处理的数据是整齐的。

再次证明，用假设小的数值，用小的例子，小的数据有助于理解，

再看规约-第二阶段进一步循环展开

使用template把上述实现的第二阶段的for循环，做循环展开，这个展开是完全的展开。思路与上述实现一样，warp同步的优化方案就更近一步了。code如下：

template<int threadsPerBlock>
__global__ void reductionKernel(int* in, int* out, size_t N){
    __shared__ int buffer[];

    // 第一步，
    int tid = threadIdx.x;
    int sum = 0;
    int id = tid + threadsPerBlock * blockIdx.x;
    int stride = threadsPerBlock * gridDim.x; 
    for (size_t i = id; i< N; i += stride){
        sum += in[i];
    }
    buffer[tid] = sum;
    __syncthreads();
    
    // 第二步，循环展开, 从1024开始，
    // 每个block最多threads个数是1024（就目前的GPU架构）
    if(threadsPerBlock >= 1024){
        if(tid < 512)   // tid 小于512 的threads开始工作
            buffer[tid] += buffer[tid + 512];
        __syncthreads();
    }
    if(threadsPerBlock >= 512){
        if(tid < 256)  // tid 小于256 的threads开始工作
            buffer[tid] += buffer[tid + 256];
        __syncthreads();
    }
    if(threadsPerBlock >= 256){
        if(tid < 128)  // tid 小于128 的threads开始工作
            buffer[tid] += buffer[tid + 128];
        __syncthreads();
    }
    if(threadsPerBlock >= 128){
        if(tid < 64)  // tid 小于64 的threads开始工作
            buffer[tid] += buffer[tid + 64];
        __syncthreads();
    }
    // 第三步。warp同步操作，不需要__syncthreads()
    if( tid<32 ){     // tid 小于32 的threads开始工作
        volatile int* wsSum = buffer;
        // 下面的6条if语句都会被执行，
        // 看第一个if的64与第二步最后的64连接上了。
        if (threadsPerBlock >= 64) wsSum[tid] += wsSum[tid + 32];
        if (threadsPerBlock >= 32) wsSum[tid] += wsSum[tid + 16];
        if (threadsPerBlock >= 16) wsSum[tid] += wsSum[tid + 8];
        if (threadsPerBlock >= 8) wsSum[tid] += wsSum[tid + 4];
        if (threadsPerBlock >= 4) wsSum[tid] += wsSum[tid + 2];
        if (threadsPerBlock >= 2) wsSum[tid] += wsSum[tid + 1];
        if (tid == 0) out[blockIdx.x] = wsSum[0];
    }
}

完全展开，避免了循环控制的开销，第三步的展开还避免了thread同步的逻辑。

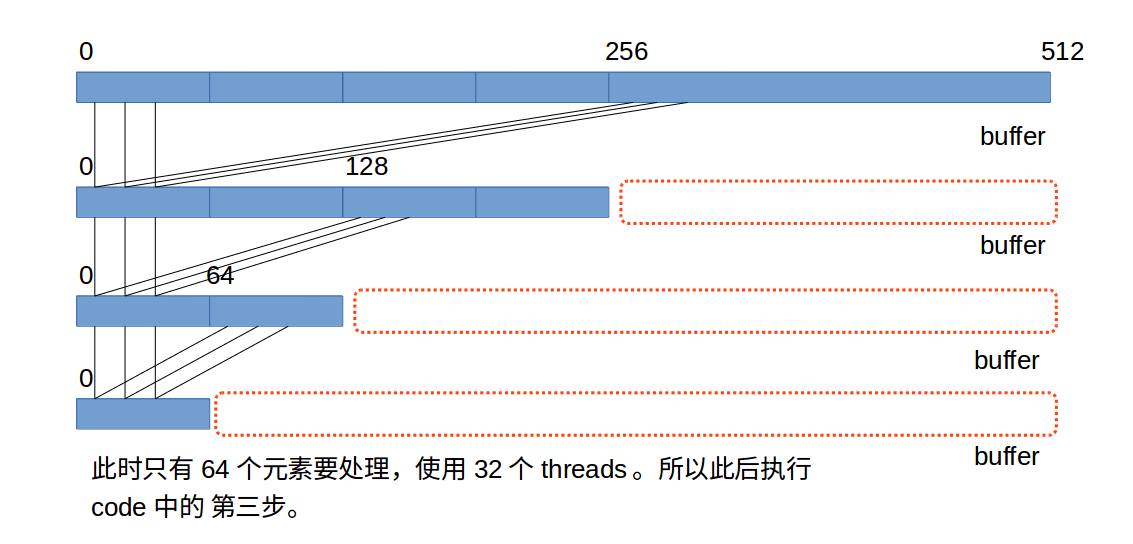
这里的执行有个特点，看if判断中的数字：1024，512，256，128，64，32，16，8，4，2，1，从逻辑看，一定是从大到小排列的，而且执行的时候，如果有一个if满足，那么这个if及其之后的if语句都会被执行。过程看下图。

第三次强调：第一阶段的blockDim.x应该是32的倍数，每个block对应的Shared memory大小也要是32的倍数。这样才能保证在第二阶段所处理的数据是整齐的。

所以设threadPerBLock为512时的示意图如下：

第三步中，不需要__syncthreads()，一个warp中的threads天然同步。

这个kernel是个模板kernel，在被host函数调用时，要指定threadsPerBlock的值。

调用kernel的host函数也必须是一个模板函数：

template<int threadsPerBlock>
void callReduction(int* res, int* partial, 
                    int* in, size_t N, 
                    int numBlocks){
    // 第一阶段，得到所有block对应的shared memory中的值
    reductionKernel<numBlocks><<<numBlocks, 
                                threadsPerBlocks, 
                                threadsPerBlocks*sizeof(int)
                                >>>(partial, in, N);
    // 两个阶段串行
    // 第二阶段，对上一步中partial中的所有值，执行规约
    reductionKernel<numBlocks><<<1, 
                                threadsPerBlocks, 
                                threadsPerBlocks*sizeof(int)
                                >>>(res, partial, numBlocks);             
}

// 使用switch语句，按照不同 block大小出发对应的模板函数。
void func(int* out, int* partial, 
            int* in, size_t N, 
            int numBlocks, int threadsPerBlock){
    switch( theadsPerBlock ){
        case 1: return callReduction< 1 >(...);
        case 2: return callReduction< 2 >(...);
        case 4: return callReduction< 4 >(...);
        case 8: return callReduction< 8 >(...);
        case 16: return callReduction< 16 >(...);
        case 32: return callReduction< 32 >(...);
        case 64: return callReduction< 64 >(...);
        case 128: return callReduction< 128 >(...);
        case 256: return callReduction< 256 >(...);
        case 512: return callReduction< 512 >(...);
        case 1024: return callReduction< 1024 >(...);
    }
}

之所以不能在一个kernel中获得最后结果，是因为，block与block之间是没有同步的。而第二阶段的规约需要所有block的buffer中第一个值，集合在一起，作为前提，如第一幅图所示。可不可以只一阶段就完成任务呢。