CUDA-原子操作-例-直方图

原子操作

atomicAdd(), atomicSub(), atomicXor()...

原子操作要排队，所以，能不用就不要使用。

原子操作-直方图

前面说过了，原子操作能不用就不使用。但是有些情况只能使用原子操作，当成千上万个threads同时修改同一个内存地址时，大规模并行系统会带来负担，在硬件中支持的原子操作可以减轻这种负担。比如计算“直方图”：计算一个数组中元素的出现频率。许多算法需要计算直方图，比如在图像处理使用过。

这里给出计算直方图的3种方法，CPU，未优化的GPU，优化后的GPU。

假如有一个很大的字符数组，实际中可能是像素的颜色值，或者是音频的采样数据。计算这个字符数组的直方图。由于每个随机的字符（一个char型占1 byte）都有2x2x2x2x2x2x2x2=256个不同的可能取值。所以直方图中要包含256个元素。

CPU版本

#define SIZE (100*1024*1024)

int main{
    // 1) 生成100MB的随机数据
    char* buffer = (char*)big_random_block( SIZE );
    // 2) 将buffer数组初始化为0
    int histo[256];
    for (int i=0;i<256;i++){
        histo[i] = 0;
    }
    // 3) 计算每个字符出现的频率
    for (int i=0;i<SIZE;i++){
        histo[buffer[i]]++;
    }
    // 4) 回收资源
    free(buffer);
    return 0;
}

不必解释。

未优化的GPU

计算直方图的特点是，读取buffer中的每一个元素，在histo数组中找到这个元素，后这个元素的频数加一，直到得到最后的直方图。如果使用并行计算，看到了吧，问题在哪？每一个thread读取buffer中不同的地址，取元素，没毛病。但是当写入histo数组时，会同时有多个threads写入histo的同一个位置，只必然造成Race condition（竞争）。所以多个threads写入同一个地址时，将写操作串行。先给出Host的主体：

int main( void ) {
    char *buffer = (unsigned char*)big_random_block( SIZE );

    char *dev_buffer;
    int *dev_histo;
    HANDLE_ERROR( cudaMalloc( (void**)&dev_buffer, SIZE ) );
    HANDLE_ERROR( cudaMemcpy( dev_buffer, buffer, SIZE,cudaMemcpyHostToDevice ) );

    HANDLE_ERROR( cudaMalloc( (void**)&dev_histo, 256 * sizeof( long ) ) );
    // dev_histo的初始化使用cudaMemset(), 将所有元素值设为0
    HANDLE_ERROR( cudaMemset( dev_histo, 0, 256 * sizeof( int ) ) );

    kernel<<<>>>();  //！！！

    int histo[256];
    HANDLE_ERROR( cudaMemcpy( histo, dev_histo, 256 * sizeof(int), cudaMemcpyDeviceToHost ) );

    // 验证GPU上计算的正确性，执行逆向运算，
    // 判断最后histo数组是否全为零（看是否可以会到初始值）
    for (int i=0; i<SIZE; i++)
        histo[buffer[i]]--;  
    for (int i=0; i<256; i++) {
        if (histo[i] != 0)
            printf( "Failure at %d!\n", i );
    }
    cudaFree( dev_histo );
    cudaFree( dev_buffer );
    free( buffer );
    return 0;
}

现在只剩下kernel函数。结果直方图数组有256个元素，所以考虑每个block含有256个threads。其实可以有其他的配置，比如100MB数据共有104,857,600个字节，所以可以启动一个block，让每个thread处理409,600个数据，或者可以启动409600个blocks，每个thread处理1个元素。

最有的配置方案介于这两种极端情况之间。实验发现，当block的数量是芯片SM数量的2倍时，将达到最有性能。

所以要先查硬件信息得到所使用GPU的SM数量：

cudaDeviceProp prop;
HANDLE_ERROR( cudaGetDeviceProperties( &prop, 0 ) ); // 使用0号GPU
int numSM = prop.multiProcessorCount;
kernel<<<numSM*2, 256>>>(dev_buffer, SIZE, dev_histo); // 未实现

下面实现kernel。

kernel的参数有三个：一个指向输入数组的指针，输入数组的长度，一个指向输出直方图数组的指针。

__global__ void histo_kernel( char *buffer,
                                long size,
                                int *histo ) {
    int i = threadIdx.x + blockIdx.x * blockDim.x;
    int stride = blockDim.x * gridDim.x;
    
    // stride loop
    while (i < size) {
        atomicAdd( &(histo[buffer[i]]), 1 );
        i += stride;
    }
}

其中atomicAdd( &(histo[buffer[i]]), 1 )展示了如何使用原子操作：atomicAdd( add, y ), 这个操作读取地址add中值，将y加到add的值上。这个例子中add就是直方图中相应元素的位置。

性能结果怎样呢？实验得GPU版本比CPU版本性能差很多倍。分析原因：

第一，kernel函数实际上只包含了非常少的计算工作，而对global的访问远远多于计算，并且对global的访问相当慢。计算少，访存多，撞上性能瓶颈。
第二，当上万个threads访问少量（256）的内存位置时，发生严重的race condition。而且原子操作为了保证结果的正确性，对于相同的内存位置都将串行化。这导致排了非常长的队伍，因此抵消了并行带来的性能提升。

所以尝试优化GPU

使用shared memory优化原子操作

主要问题并不是使用了过多的原子操作，而是有太多的threads写入太少的地址造成的竞争。考虑使用两段操作。

为方便画图表示，假如元素只有x，y，z三种字符。那么自然地，每个block使用3个threads干活，对应的Shared memory大小也为3。假设block个数是2。两阶段如下图：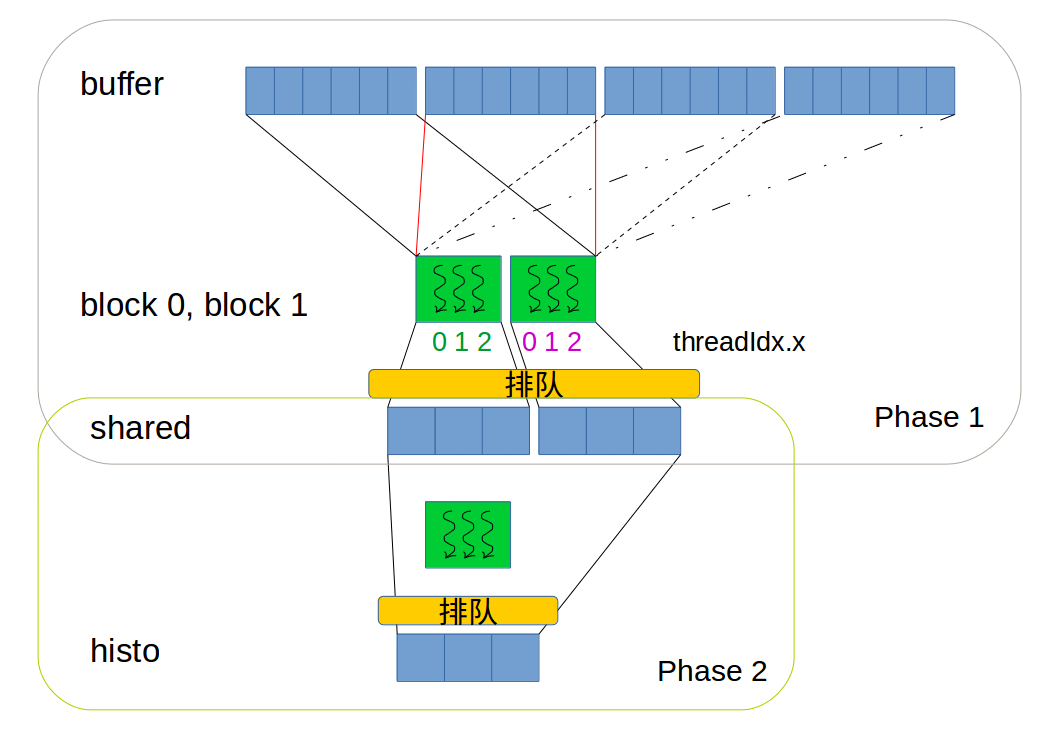

过程如下：

第一段，让每个并行的block计算它所处理的数据，将结果写入各自block对应的shared memory中。这样做的好处有：

第一，所有blocks之间的计算是并行的。
第二，写入shared memory效率远高于写入global memory。

第三，这种方式仍然需要原子操作，但是此时是256个threads在256个地址上的竞争，竞争程度显著减少。

所以，第一阶段计算得到每个block的临时直方图，比如，有三个blocks, 那么遍历完所有元素后会得到三个临时直方图。当得到所有三个临时直方图后（要同步），开始第二个计算阶段。

第二段，将得到的全部临时直方图合并为最终直方图，也应该是原子操作。这一段是，会有block数量个threads在256个地址上的竞争，竞争程度又显著减少。

__global__ void histo_kernel( char* buffer,
                                long size,
                                int* histo ) {
    // 初始化
    __shared__ unsigned int temp[256];
    temp[threadIdx.x] = 0;
    __syncthreads();

    int i = threadIdx.x + blockIdx.x * blockDim.x;
    int offset = blockDim.x * gridDim.x;
    // 第一段计算
    while (i < size) {
        atomicAdd( &temp[buffer[i]], 1 );
        i += offset;
    }
    __syncthreads();

    //第二段计算
    atomicAdd( &(histo[threadIdx.x]), temp[threadIdx.x] );
}

// kernel 的配置如下
kernel<<<numSM*2, 256>>>(dev_buffer, SIZE, dev_histo);

在实际SP和threads执行中，上述代码（指令）被复制很多份，有多少个threads就复制多少份。这些拷贝的不同在于，threadIdx.x，blockIdx.x这些值会被自动赋值，0, 1, 2, 3, ...

性能如何？比CPU版本的快了一个数量级。

总结：使用了一种两阶段的算法，从而降低了在global memory上访存的竞争程度。这种降低竞争的策略总能获得不错的效果，所以当使用原子操作时，记住这种操作。