扫描算法
Scan,是并行编程的一个重要原语,作为基本模块使用与很多不同的算法。Scan做的是什么事呢?看下例:
1
2
3
4
5
| input:
[a0, a1, a2, a3, ..., an]
output:
[a0, (a0+a1), (a0+a1+a2), ..., (a0+a1+a2+...+an)]
|
其特点是,输出的每一个值有前缀依赖性,就是说每个输出依赖前面的所有输入。两种基本的扫描的过程如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| template<class T>
T scan1(T* out, T* in, size_t N){
T sum = 0;
for int i=0;i<N;i++){
sum += in[i];
out[i] = sum;
}
}
template<class T>
T scan2(T* out, T* in, size_t N){
T sum=0;
for(int i=0;i<N;i++){
out[i] = sum;
sum += in[i];
}
}
|
不多解释。
Blelloch并行扫描算法
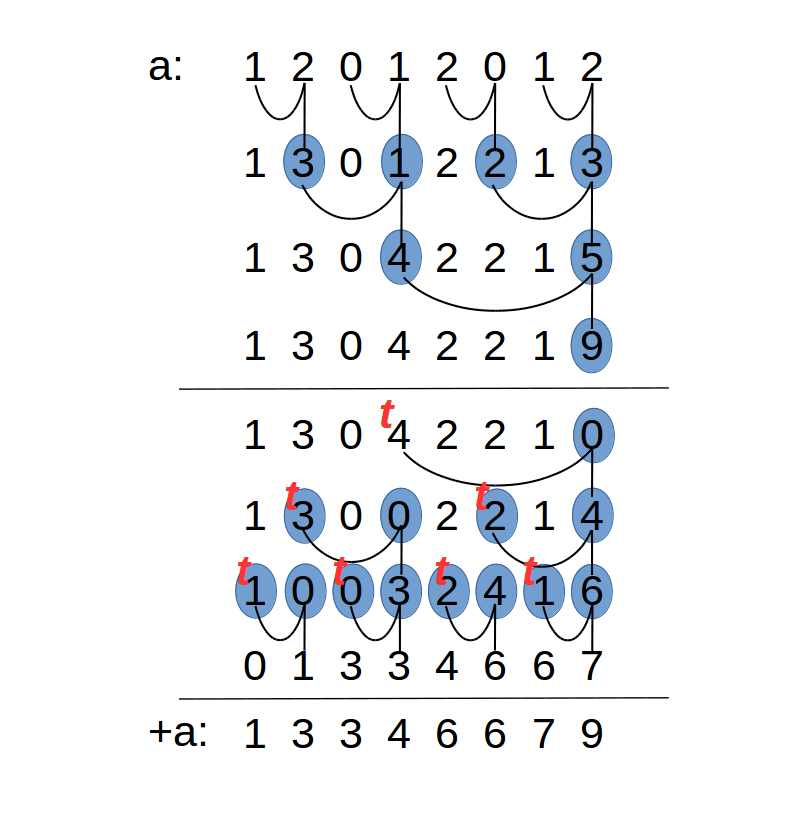
这个方法在前元素后依赖的情况下,并行实现。Blelloch算法分了两段执行。过程如下图:
两个阶段的伪代码:
阶段一
1
2
3
4
5
6
| (int* a, int N){
int d;
d 从0到(logN-1):
并行:i从0到(N-1),步长2**(d+1):
a[i+2**(d+1) -1] += a[i+2**d -1];
}
|
阶段二:
1
2
3
4
5
6
7
8
9
| (int* a, int N){
a[N-1]=0
int d;
d 从(logN-1)到0:
并行:i从0到(N-1),步长2**(d+1):
t = a[i+2**d -1];
a[i+2**d -1] = a[i+2**(d+1) -1];
a[i+2**(d+1) -1] += t;
}
|
将得到的数组与原数组相加的最终结果。
每个阶段的操作虽然容易想到,但是,这个框架是很值得借鉴的。图中实例,每两行之间的操作是并行的,而且这两行之间的并行操作必须全部执行完毕,才能向下执行,所以需要同步操作,尤其是当存在线程ID更新时。