CUDA

CUDA-并行一维卷积

卷积操作应用于许多领域，而其特点：计算量大，每个输出元素的计算都是相互独立的。这两个特点是并行计算期望处理的。卷积中对于边界的处理影响着分块算法的效率。

一维卷积基本形式

假设一维数组N是被操作对象，一维数组M是卷积核，一维数组P为卷积结果。假如对于边界元素（幽灵元素）的处理是赋值为0，也就是说幽灵元素与对应的M元素的乘积为0.

若每个thread负责P数组中的一个元素，那么一维卷积的基本形式如下图：

图：一维卷积基本形式

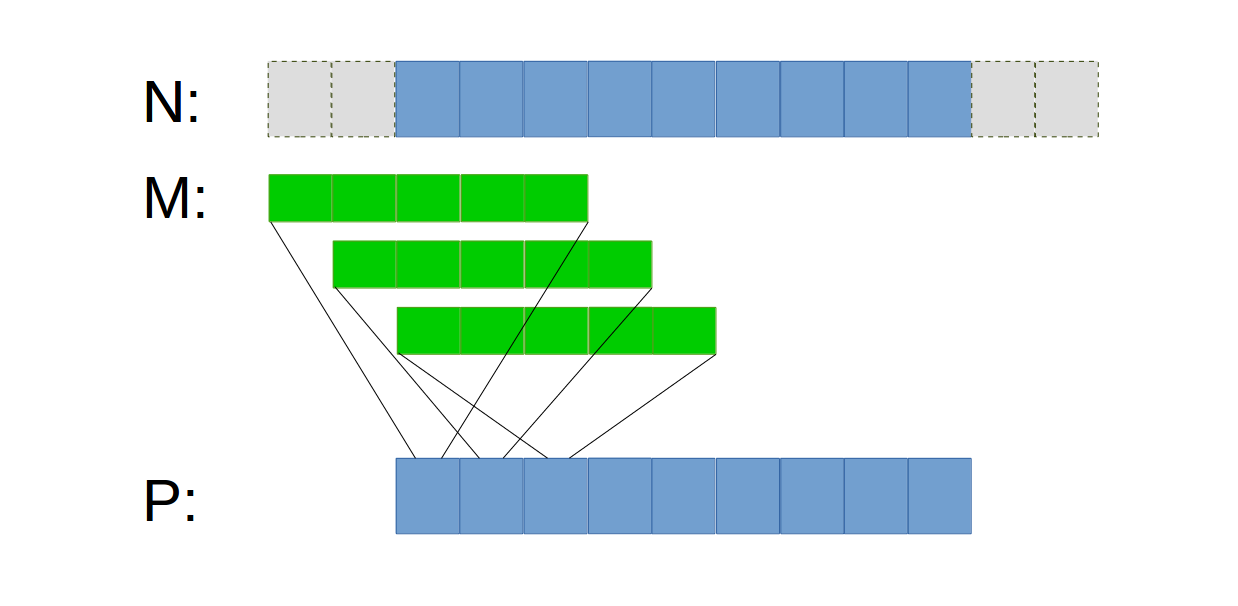
一个thread得到结果数组P中一个元素。实现：

1
2
3
4
5
6
7
8
9
10
11
12
__global__ void conv1D(float* N, float* M, float* P, 
                        int kernelSize, int NLength){
    int tid = threadIdx.x + blockDim.x * blockIdx.x;
    float Pvalue = 0.0f;
    int start = tid-kernelSize/2;
    for (int j=0; j<kernelSize; j++){
        if(start + j >= 0 && start + j <= NLength){
            Pvalue += N[start + j] * M[j]; 	
        }
    }
    P[tid] = Pvalue;
}

一般卷积核的长度是奇数，这样计算过程是对称的。

上述实现的缺点：

  • 代码中这句 Pvalue += N[start + j] * M[j]包含两次对Global 的访存，和两次算术运算（一个乘法，一个加法）。运算访存比仅为1.0。性能有限。
  • 对边界的处理出现Divergence。

Constant Memory优化的一维卷积

卷积操作有三个特点：

  1. 考虑到卷积计算的过程，以及实际中的卷积操作，比如在Google Inception Net分组卷积，MobileNet深度可分离卷积，ResNet中的残差学习单元，中的描述，卷积核大小都是3x3, 1x1, 1x7, 7x1，5x5很小的卷积核。
  2. 卷积核的内容是不变的。
  3. 所有的threads都访问卷积核（假设就一个卷积核），并且访问卷积核中元素的顺序是一样的。

根据这些特点结合Ray-Tracing这篇笔记中Constant Memory
描述的Constant Memory的特性。考虑将卷积核放入Constant Memory。

这里补充一点，Constant Memory中的内容对于所有Blocks可见。使用.totalConstMem可以查询其大小。

与Ray-Tracing中的使用一样：

1
2
3
4
5
6
7
8
9
#define MAX_KERNEL_LENGTH 10;
__constant__ float M[MAX_KERNEL_LENGTH];

...

// 在main函数中使用cudaMemcpy的特殊版本函数
cudaMemcpyToSymbol(M, h_M, kernel_length*sizeof(float));

...

kernel函数与基本形式一样，除了参数列表中不需要再传入卷积核数组M。

虽然Constant Memory在Global中，但是cuda知道Constant Memory中的内容是不变的。所以直接将其放入高速缓存中（L1缓存）。

补充:
高速缓存的层次结构。从DRAM中访问一个变量需要数百上千个时钟周期，而且处理器处理数据要比访存快得多。DRAM的长延迟和有限带宽成了现代处理器的性能瓶颈，称为存储器墙。现在的处理器都会有片内的高速缓存，来减少DRAM的访存次数。

缓存一致性:
使用高速缓存的一个重要设计问题是缓存一致性，当一个或多个处理器核心试图修改缓存中的数据时，问题出现了。每一个处理器核心有自己的L1缓存，如果这个被修改了，而其他核心的L1缓存不变，缓存中的内容就不一致了。在并行处理器中处理缓存一致性开销很大（就相当于实现全局线程同步开销很大一样）。所以GPU中没有缓存一致性的机制。

将Constant memory放到L1高速缓存中。WHY

  • Constant memory中的内容在kernel执行期间不会被改变，因此没有缓存一致性的问题干扰。所以硬件可以直接将Constant memory放到L1高速缓存中。
  • 在处理器的缓存设计中通常优化了线程的广播。所以当一个warp中的线程访问同一个Constant memory中的（相同的）变量时，高速缓存能为threads所需要的数据提供巨大的带宽。

Shared memory优化的分块并行卷积

分析卷积过程，以一维卷积为例，假设卷积核的长度是5，N（Global）中有100个元素，其中每一个元素要平均被访问5次，那么就需要500次的Global memory的访存。显然，N中每个元素被重复访问了。所以考虑是用分块Shared memory来降低Global的访存。

假设N长度为15，M长度为5，block大小为4，Shared memory大小为4，输出到P。过程如下图：

<>pic2<>

图：一维分块卷积 回顾时添加

每一个thread处理一个P中元素，对于每一个block，分两步操作：

  1. 将数据从N中写入blocks对应的Shared 中。
  2. 执行卷积计算。

而读入Shared的操作分为左中右，三部分

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#define KERNEL_LENGTH 5;
__constant__ float M[KERNEL_LENGTH]; // 卷积核

__global__ void Convolution(float* N, float* P, int N_size){
    __shared__ float N_ds[TILE_SIZE + KERNEL_LENGTH-1];
    int tid = threadIdx.x + blockDim.x * blockIdx.x;
    int n = KERNEL_LENGTH/2;

    // 读左
    int left = (blockIdx.x -1)*blockDim.x + threadIdx.x;
    if(threadIdx.x >= blockDim.x - n){
        N_ds[threadIdx - (blockDim.x - n)] = (left<0) ? 0 : N[left];
    }
    // 读中
    N_ds[n+threadIdx.x] = N[tid];

    // 读右
    int right = (blockIdx.x + 1)*blockDim.x + threadIdx.x;
    if(threadIdx.x < n){
        N_ds[n+blockDim.x+threadIdx.x] = (left>=N_size) ? 0 : N[right];
    }

    __syncthreads();
    // 卷积操作
    float Pvalue = 0.0f;
    for(int i=0;i<KERNEL_LENGTH; i++){
        Pvalue += N_ds[threadIdx.x + i] * M[i];
    }
    P[tid] = Pvalue;
}

L2缓存了的分块并行卷积

新知
上个实现的代码复杂度集中在了将左右元素加载到Shared 中，注意，一个block的左右元素，同时又是相邻block的内部元素，因此很有可能在block #1需要这些左右元素时，它们已经由于block #2的访问而存储到了L2缓存上。这样对于左右元素的访问从代码上是访问了global，实际上却是转化为对L2缓存的访问。依然达到减少Global访存的目的。看下图：

<>pic3<> 图8-10

图 回顾时添加

如此一来，shared memory 的大小变成如下，与block的大小一致了：

1
__shared__ float N_ds[TILE_SIZE];

从而Shared memory的加载就更简单了：

1
2
int tid = threadIdx.x + blockDim.x * blockIdx.x;
N_ds[threadIdx.x] = N[tid];

之后就是对于每一个thread遍历卷积核中元素，乘累加。只是对于中间元素，已经存在于自己的Shared中了，访问自己的Shared；对于左右元素，访问N，实际上是访问L2 缓存。

实现与基本形式相似：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#define KERNEL_LENGTH 5;
__constant__ float M[KERNEL_LENGTH]; // 卷积核

__global__ void Convolution(float* N, float* P, int N_size){
    __shared__ float N_ds[TILE_SIZE];

    int tid = threadIdx.x + blockDim.x * blockIdx.x;
    N_ds[threadIdx.x] = N[tid];

    __syncthreads();
    int this_block_start = blockIdx.x * blockDim.x;
    int next_block_start = (blockIdx.x+1) * blockDim.x;

    int n_start = tid-(KERNEL_LENGTH/2);
    float Pvalue=0.0f;
    // 遍历卷积核：
    for(int j=0;j<KERNEL_LENGTH; j++){
        int index = n_start + j;
        // 对于有效Index：
        if(index>=0 && index<=N_size){
            // 对于中间元素：
            if((index >= this_block_start) && (index < next_block_start)){
                Pvalue += N_ds[threadIdx.x + j-KERNEL_LENGTH/2]*M[j];
            }else{  // 对于左右元素：
                Pvalue += N[index]*M[j];
            }
        }
    }
    P[tid] = Pvalue;
}

敲黑板

  • 所有这些技术都可以用在二维，三维卷积，只不过是对存储访问的索引计算更加复杂。
  • 存在对Global的重复访问，考虑使用Shared。
  • shared memory在L1缓存中。
  • 考虑元素是否被缓存到L2.
  • 缓存：作为名词是指在芯片内部的高速存储区域；作为动词指将其他存储空间中的内容放入高速缓存空间。[待求证]