• 类似，生病了找多名专家从不同方面一起确诊。
• 集成学习将多个学习器进行结合，通常可以获得比单一的学习器更优的泛化性能。
• 集成学习可以得带3中不同结果：提升性能，不起作用，起负作用。
• 所以要想获得好的集成结果，每个学习器应该“好而不同”，即每个学习器要有一定的准确性，同时，每个学习器各不相同。即“多样性”。
• 实际上，如何产生“好而不同”的基学习器，是集成学习的核心。

构建

使用数据集：

1

x, y = datasets.make_moons(n_samples=500, noise=0.2, random_state=321)

构建三个基学习器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

#1） 使用逻辑回归
from sklearn.linear_model import LogisticRegression
log = LogisticRegression()
log.fit(x_train, y_train)
print(log.score(x_test, y_test))   #  0.896

#2) 使用SVM
from sklearn.svm import SVC
svm = SVC()
svm.fit(x_train, y_train)
print(svm.score(x_test, y_test))   #  0.952

#3) 使用决策树分类
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier()
tree.fit(x_train, y_train)
print(tree.score(x_test, y_test))  #  0.944

结果分别为 0.896, 0.952, 0.944.

投票操作：

1
2
3
4
5
6
7
8
9
10
11
12

# voting
y_pre1 = log.predict(x_test)
y_pre2 = svm.predict(x_test)
y_pre3 = tree.predict(x_test)

# 少数服从多数
# 对于三个模型的预测值，至少2个模型判断它为1，我才认为它是1：
y_p = np.asarray((y_pre1 + y_pre2 + y_pre3) >= 2, dtype=int)
print(y_pre1[:10])   #  [1 1 1 1 1 0 1 0 0 0]
print(y_pre2[:10])   #  [1 1 1 1 1 0 1 0 0 1]
print(y_pre3[:10])   #  [1 1 1 1 1 0 1 0 0 1]
print(y_p[:10])      #  [1 1 1 1 1 0 1 0 0 1]

判断集成效果：

1
2
3

from sklearn.metrics import accuracy_score
acc = accuracy_score(y_test, y_p)
print(acc)     #  0.96

最终集成性能是0.96。

Hard voting

hard voting 即少数服从多数：

1
2
3
4
5
6
7
8
9
10

from sklearn.ensemble import VotingClassifier

voting = VotingClassifier(estimators=[
    ('log', LogisticRegression()),
    ('svm', SVC()),
    ('tree', DecisionTreeClassifier())
], voting='hard')

voting.fit(x_train, y_train)
print(voting.score(x_test, y_test))    #  0.96

实际中，通常把基学习器调参到最优，后再集成。

Soft voting

hard voting 其实是“少数服从多数”，而 soft voting 带权投票，如歌唱的专业评审团的投票权重就大。如：

5个学习器把同一个样本分为A类或B类的概率分别如下：

            A类    B类
学习器#0   99.0%  1.0%
学习器#1   49.0%  51.0%
学习器#2   43.0%  57.0%
学习器#3   98.0%  2.0%
学习器#4   34.0%  64.0%

如果使用hard voting 该样本最终本分为B类。

但是，显然学习器#0和#3有很大的把握认为该样本属于A类，而其他三个学习器并没有很确定该样本的类别。所以“少数服从多数”不合适。使用Soft voting 计算
属于A类：(99.0%+49.0%+43.0%+98.0%+34.0%) / 5 = 64.6%.
属于B类：(1.0%+51.0%+57.0%+2.0%+64.0%) / 5 = 35.0%.
所以该样本应该被分类为A。

使用 Soft voting 的基学习器要求都应该估计概率，即可以调用 predict_proba 函数。SVM模型把probability设为true，便可以进行概率估计。调用VotingClassifier时指明voting方式为soft即可：

1
2
3
4
5
6
7
8
9

from sklearn.ensemble import VotingClassifier
voting2 = VotingClassifier(estimators=[
    ('log', LogisticRegression()),
    ('svm', SVC(probability=True)),
    ('tree', DecisionTreeClassifier())
], voting='soft')

voting2.fit(x_train, y_train)
print(voting2.score(x_test, y_test))   #  0.976

所以，当基学习器可以求出样本概率估计时，Soft voting 比 hard voting 性能优。

敲黑板理解当前问题，才能找到已有方法的不足，才能找到更合适的方法。就如本文表达的用Soft voting 替代已有的Hard voting。

• 决策树是非参数学习算法
• 天然解决多分类问题
• 有很好的可解释性
• 关键问题是使用哪个特征做为根节点
• 对于连续值的特征，在哪个值上做划分

离散数据集

使用iris数据集，调用sklearn的Decision Tree 模型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

iris = datasets.load_iris()

# 只是用数据2个特征
x = iris.data[:, 2:]
y = iris.target

from sklearn.tree import DecisionTreeClassifier

tree_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy")
tree_clf.fit(x, y)

plot_decision_boundary(tree_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(x[y == 0, 0], x[y == 0, 1])
plt.scatter(x[y == 2, 0], x[y == 2, 1])
plt.scatter(x[y == 1, 0], x[y == 1, 1])
plt.show()

结果：

划分后使得系统的熵（即不确定性）降低。所以对于一个划分，如果划分后的系统信息熵比其他划分后的熵都要小，则当前就是用这个划分。根据这个原理，可以就特征为连续值的数据集进行划分：

连续值的数据集

已知特征d，和value， 对x进行划分：

1
2
3
4

def split(x, y, d, value):
    index_a = (x[:, d] <= value)
    index_b = (x[:, d] > value)
    return x[index_a], x[index_b], y[index_a], y[index_b]

传入label列表，求此时的系统信息熵：

1
2
3
4
5
6
7
8
9
10
11

from collections import Counter
from math import log2

def cal_entropy(y):
    # counter 为字典，[类别，这个类别所含样本数]
    counter = Counter(y)  
    res = 0.0
    for num in counter.values():
        p = num / len(y)
        res += -p * log2(p)
    return res

定义一次划分，即，划分算法：搜索找到使得熵最小的特征d和value：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

def try_split(x, y):

    # 初始值最大
    best_entropy = float('inf')  
    # best_e_l, best_e_r = -1, -1
    # 初始化d 和 value
    best_d, best_v = -1, -1   
    # 在x 的所有维度（特征）搜索d：
    for d in range(x.shape[1]):
        # 在特征d的哪个值上划分：先排序，后找相邻的样本在特征d上的中间值是多少
        sorted_index = np.argsort(x[:, d])
        for i in range(1, len(x)):  # 遍历所有样本
            if x[sorted_index[i-1], d] != x[sorted_index[i], d]:
                v = (x[sorted_index[i-1], d] + x[sorted_index[i], d]) / 2
                # 有了 d 和 v， split：
                x_l, x_r, y_l, y_r = split(x, y, d, v) 
                # 此时系统熵是多少
                e = cal_entropy(y_l) + cal_entropy(y_r)
                # e_l = cal_entropy(y_l)
                # e_r = cal_entropy(y_r)
                # 判断新的熵e是否小于best_entropy，更新best_entropy
                if e < best_entropy:
                    best_entropy, best_v, best_d = e, v, d

    return best_entropy, best_d, best_v

调用函数得第一次划分：

1
2
3
4
5
6

# 第一次划分：
best_entropy, best_d, best_v = try_split(x, y)
x1_l, x1_r, y1_l, y1_r = split(x, y, best_d, best_v)

print(cal_entropy(y1_l))  # 0.0  
print(cal_entropy(y1_r))  # 1.0

左子树的熵为0，右子树的熵大于0，所以对右子树进行第二次划分：

1
2
3
4
5
6

# 对于右边再次划分：
best2_entropy, best2_d, best2_v = try_split(x1_r, y1_r)
x2_l, x2_r, y2_l, y2_r = split(x1_r, y1_r, best2_d, best2_v)

print(cal_entropy(y2_l))  # 0.44506485705083865
print(cal_entropy(y2_r))  # 0.15109697051711368

可以继续深入划分。

由于数据集各个特征值是连续的，所以，上述过程是：遍历找到所划分的特征，这个特征中遍历的所有样本，排序后求相邻两个样本的均值作为这个特征的具体划分值，时间复杂度为O(mxn)，即样本个数乘以特征个数。

对于各个特征值为离散的，使用信息增益来找到消除不确定性最强的特征。每次都找信息增益最大的属性作为下一个划分属性。

升维

在现实任务中，样本空间内很可能不存在一个能将样本正确划分的超平面。此时，可以将样本从原始空间映射到一个更高维的样本空间，使得样本在这个高维空间内线性可分。如果原始空间是有限维的，也就是说，样本的属性个数有限，那么一定存在一个更高的样本维度使样本线性可分。

上述涉及到每一个特征映射到高维空间后之间的内积，由于特征空间的维度可能很高，甚至是无穷维的，因此先映射到高维空间后计算，是非常困难的。即，核函数可以等价代替样本映射后的特征向量间的内积。使用Kernel Trick 避开这个障碍。如此用一个近似的计算来取代映射到高维特征向量。好处：减少了计算量，节省了内存，Kernel Trick是一个可以应用于任何算法的技巧。

RBF核

假如原始数据只有一维信息，如果有两个landmark，就将数据变化为2维数据。每个样本的取值变化为x->( ，)，即含有2个特征。下面模拟该过程：

1
2
3
4
5
6
7
8
9

# 一维数据x
x = np.arange(-10, 10, 1) 

# 对应的lable
y = np.asarray((x >= -3) & (x <= 3), dtype=int)

plt.scatter(x[y == 0], 0*(y[y == 0]))
plt.scatter(x[y == 1], 0*(y[y == 1]))
plt.show()

如图：

定义一个函数，每个样本跟landmark进行计算，得到新的x：

1
2
3
4
5
6
7
8
9

def gaussian(x, l):
    """
    每个x 跟l计算得到新的x
    :param x: 原来x
    :param l: x跟谁计算
    :return: 新的x
    """
    gamma = 0.05
    return np.exp(-gamma * (x - l)**2)

对x的每个样本进行升维处理，得到新的x：

1
2
3
4
5
6
7
8
9
10
11

x_new = np.empty((len(x), 2))

for i, data in enumerate(x):
    # x_new 的第一个特征：
    x_new[i, 0] = gaussian(data, 1)
    # x_new 的第二个特征：
    x_new[i, 1] = gaussian(data, -1)

plt.scatter(x_new[y == 0, 0], x_new[y == 0, 1])
plt.scatter(x_new[y == 1, 0], x_new[y == 1, 1])
plt.show()

如图：

此2维数据显然是线性可分的。本例是使用l1和l2 两个landmark，即，只将数据变化为2维，原本20x1的数据映射成20x2。BRF高斯核实际上是使用每一个数据点作为landmark，即原本mxn的数据映射成mxm的数据。当m远远大于n时(一般合格的数据集)，数据特征由n增加到m。当然，对于一个m小于n的数据集(如NLP等情境下的数据)，依然变换为mxm，其实是降维处理。

RBF核gamma

RBF中的参数gamma与高斯分布有关：gamma越大，分布越窄越高。
实验如下：

1
2
3
4
5
6
7

# 使用moon数据：
x, y = datasets.make_moons(noise=0.15, random_state=11)

# 定义模型：
def RBFKernel(gamma=0.1):
    return Pipeline([("standard", StandardScaler()),
                     ("svc", SVC(kernel="rbf", gamma=gamma))])

指定gamma，并学习，当gamma=100时：

1
2
3
4
5
6

svc = RBFKernel(100)
svc.fit(x, y)
plot_decision_boundary(svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y == 0, 0], x[y == 0, 1])
plt.scatter(x[y == 1, 0], x[y == 1, 1])
plt.show()

绘图：

当gamma=100，很大， 对应高斯分布越高越窄， 反映在图中就是每一个橘色样本点周围的小区域为一个高斯分布，橘色样本点本身为分布的顶点，即，模型判断，样本点只在这样一个区域内，才被判定为橘色点。 此情况显然过拟合。

当gamma=10， 上述的分布区域变大了：

当gamma=0.1，很小时，不拟合：

所以可以说，gamma值在控制模型的复杂度，gamma越小，模型复杂度越小，
所以要找到合适的gamma。

SVM解决回归问题：SVR

SVR 使得在margin范围里的样本点越多越好，表示这个范围可以较好地表示样本点。此时取中间的线为回归曲线。

或者说，SVR解决的问题与SVM相反，soft SVM要使得margin间的点越少越好，而SVR要使得margin间的点越多越好。

又或者说，SVR目的与SVM相同，都是最大化margin间的距离。SVR假设我们可以容忍f(x)与y之间最多有epislon的偏差，即，当且仅当f(x)与y之间的距离绝对值大于epsilon时，才计算损失，损失仍是最小化margin间的距离。这个过程相当于构建了宽度为2×epsilon的间隔带，如果样本点在间隔带之间，则认为是被预测正确的。

sklearn中的使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

from sklearn.svm import LinearSVR
from sklearn.svm import SVR  # 指明核函数
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline


def StandardLinearSVR(epsilon=0.1, c=1):
    """
    指明参数 epsilon 和 C 等
    """
    return Pipeline([
        ("standard", StandardScaler()),
        ("LinearSVR", LinearSVR(epsilon=epsilon, C=c))
    ])

对于线性不可分而非线性可分的数据，也可以使用线性SVM。只需要将数据转换为高维的含有多项式项的数据。

数据集

先找一个，分线性可分数据集：

1
2
3
4
5
6
7
8

from sklearn import datasets

x, y = datasets.make_moons(noise=0.15, random_state=11)

# 绘制出结果：
plt.scatter(x[y==0, 0], x[y==0,1])
plt.scatter(x[y==1, 0], x[y==1,1])
plt.show()

结果：

含多项式特征的LinearSVM

指定多形式的阶数，将数据转化成高维的含有多项式项数据，后传入LinearSVM：

1
2
3
4
5
6

def PolynomialSVC(degree, C=0.1):
    return Pipeline([
        ("Poly", PolynomialFeatures(degree=degree)),
        ("standard", StandardScaler()),
        ("LinearSVC", LinearSVC(C=C))
    ])

使用Pipline可以顺序执行各部分。实例化模型，并查看模型信息：

1
2
3

poly_svc = PolynomialSVC(3)
poly_svc.fit(x, y)
print(poly_svc)

模型信息：

1
2
3
4
5

Pipeline(memory=None,
     steps=[('Poly', PolynomialFeatures(degree=3, include_bias=True, interaction_only=False)), ('standard', StandardScaler(copy=True, with_mean=True, with_std=True)), ('LinearSVC', LinearSVC(C=0.1, class_weight=None, dual=True, fit_intercept=True,
     intercept_scaling=1, loss='squared_hinge', max_iter=1000,
     multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
     verbose=0))])

绘出分类边界：

1
2
3
4

plot_decision_boundary(poly_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y==0, 0], x[y==0,1])
plt.scatter(x[y==1, 0], x[y==1,1])
plt.show()

结果为分线性边界：

多项式核函数

SVM可以直接使用数据的多项式特征，即多项式核函数，所以使用SVC而非LinearSVC。此时Pipline中不需先得到多项式特征：

1
2
3
4
5
6
7

from sklearn.svm import SVC

def Polynomial_KernelSVC(degree, C=0.1):
    return Pipeline([
        ("standard", StandardScaler()),
        ("kernelSVC", SVC(kernel="poly", degree=degree, C=C))  
    ])

传入kernel参数，指定使用什么样的核函数。实例化模型，绘制分类边界：

1
2
3
4
5
6
7

poly_kernel_svc = Polynomial_KernelSVC(degree=5)
poly_kernel_svc.fit(x, y)

plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y==0, 0], x[y==0,1])
plt.scatter(x[y==1, 0], x[y==1,1])
plt.show()

边界：

香浓认为，对于一条信息，重要的是找出这条信息中含有多少信息量，要搞清楚信息量，就要找到一个量化度量信息的单位。香浓的最大贡献就是找到了这个单位“比特(bit)”。
比特是度量信息量的基本单位。它可以被这样定义：如果一个黑盒子里由A和B两种可能，而且这两种可能出现的概率相同。那么要搞清楚黑盒子中到底是A还是B，所需要的信息量就是一个比特(bit)。
当A和B的出现的概率不相同时，确定他们谁出现所需的信息量就不到一个比特。

比如，设抛一枚两面质地均匀的硬币为一个系统，状态A和B分别是正面朝上和反面朝上。则确定一次投掷所需要的信息量为一个比特。
可以这样计算：

又比如，做一道4(有A,B,C,D4中状态)选一个的选择题，需要多少信息量才能找到正确答案。2bits。先使用1bit信息确定比如是否在A或B中，若是，再使用1bit信息量确定是否是A，若否，则最终答案是B。(这只是一种判断出结果的方法，但每种方法所需的信息量都是2bits)：

所以，如果由32个足球队参加世界杯，最终需要5bits的信息量确定最终哪支球队为冠军。

可以看出的规律：一棵树，以所有可能情况为根，平均分所有情况给左子右子，如此递归，直到每个叶节点只有一种情况。此时得到树的深度即为确定做种是哪种情况所需的信息量。以选择题为例：

树的深度为2，从树根到树叶需要2步走，即需要2bits信息确定究竟是哪一个。

我们把充满不确定性的盒子称作“信息源”，它里面的不确定性称作“信息熵”，“信息”是用来消除这些不确定性的(信息熵)。所以要消除黑盒子里的不确定性，需要的“信息量”等于“信息熵”。“熵”是热力学的概念，它表示混乱程度，同样的，信息论中的信息熵表示一个系统中的不确定性。

一个系统中的状态数量也叫做可能性数量，越多，系统不确定性越大；当状态数量确定时，各个状态的可能性相同，熵达到最大；相反，如果只要概率有不相同，系统不确定性就会减小，极限情况下，当状态A发生的概率为99.9%，而其他所有状态发生的概率和为0.01%时，系统的不确定性很小：很大的概率上A是会发生的。香浓用以下公式可以计算出系统信息熵：

以二分类为例，下图体现了一个状态的概率与系统的信息熵的关系：

当状态概率为0.5时，系统信息熵，即不确定性达最大值。实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 根据上述信息熵计算公式
def entropy(p):
    return -p * np.log2(p)-(1-p)*np.log2(1-p)

x = np.linspace(0.01, 0.99, 200)

plt.plot(x, entropy(x))
# 绘出一个点
plt.scatter([0.5], [1], marker='o', edgecolors='r')   
# 添加注释 
plt.text(0.5, 1, (0.5, 1), ha='center', va='bottom', fontsize=10)   
plt.xlabel('Pr(x)', fontsize=10)
plt.ylabel('Entropy', fontsize=10)
plt.show()

在构建ID3决策树时，就是根据信息熵公式，得到各种划分后的信息熵，选取信息熵最小的划分。即这个划分使得系统不确定性变得最小！

如四选一选择题，假如，每种选项的概率均为0.25，根据公式，消除选择题的不确定性所需信息量为2bits。
如果4中选项的概率不相同，不论哪种情况，信息熵均小于2bits。

通过平衡二叉树来理解信息量单位比特。如果一个分类模型在一个数据集上的正确率为0.5，那么可以说，这个模型是最糟糕的模型，它对减少系统信息熵没有贡献。

补充

热力学熵和信息熵的物理意义，数学形式，完全一样，不存在本质区别，只是应用领域不同。克劳修斯形式(熵的宏观形式)用于内燃机研究，进入量子时代后主要使用玻尔兹曼形式(熵的微观形式)。
玻尔兹曼熵与信息熵的唯一不同只是前者计算对数用e为底数得到单位为nats，后者计算使用2为底数得到单位为bit。

另外，取10为底，得到单位是bans。其实，在决策树的计算中，求信息熵的对数底可以使任意的，因为具体在划分的时候，不管底取多少，H这个函数的性质是不会变的。模型其实在意熵的相对值，而非绝对值。

熵增原理：任何孤立的系统，总熵不会减少。

本笔记是风格转换应用的概述。

本应用需要使用使用已训练好的VGG16网络的结构及参数。VGG16.npy文件中保存了网络的结构和参数，这些参数可以通过解析网络得到，之后便可以重构整个网络，包括每一个conv layer，每一个pooling layer，每一个fully connected layer和flatten layer，以及每一层所需的w，b。如下图：

有了每一层的参数，可以构建若干conv layer 和 pooling layer。 由于本应用不使用flatten layer 和 fc layer 的输出结果，而且VGG16 大部分的参数集中在fc layer，所以不用构建此二层。

当含有训练好参数的网络构建好后，或者说函数y=f(x)及所有参数都定义好了。此时当输入f(x)一个x，便可以得到一个对应的y。

本应用需要使用三个一模一样网络y=f(x)，一个传入content_img，可以得到f(p)每一层的输出；第二个网络传入style_img，可以得到f(a)的每一层输出；第三个网络传入自变量x，f(x)。x是一个2D向量，其初始值为一个随机初始化的向量。本应用就是使随机化的x通过学习逐渐变成一个混合content_img和style_img的图像。

这个应用实际上也是个学习的过程，此过程需要3个Loss值：Lcontent，Lstyle，Ltotal。其中Lcontent是p传入f在M层的输出与x传入f在同一层的输出做平方差；Lstyle是a传入f在N层的输出的Gram矩阵与x传入同一层的输出的Gram矩阵的平方差；最后得到整个学习过程的Loss函数Ltotal：Ltotal=alpha*Lcontent+beta*Lstyle。Ltotal是一个以x为参数的函数，通过不断更新x的值来最小化Ltotal。同样是学习过程，不同于CNN应用在分类问题，Loss是以x为学习参数，w和b是定值，每次学习都是更新x。

迭代数学公式

实验通过改变alpha 和 beta的值来改变风格转化的程度。特别的，当alpha！=0，beta=0时，Ltotal只与Lcontent有关，这种情况下，学习过程变成了：x通过学习逐渐变成p(content img)；当alpha=0，beta！=0时，x通过学习逐渐变成a(style img)。

有趣的是，要想使x学习成p，需要使用f(p)在浅层的输出值；而要想是x学习成a，需要使用f(a)早深层的输出值。所以最终为了使混合图像的效果好，f(p)使用浅层输出，f(a)使用深层输出。

更新 thread ID

当数据个数 ≥ CUDA core 个数时，thread id 不用更新，一次同时习性完。

如我有2024个数据，而我的GPU每次可分配2048个threads。我的kernel配置<<<1, 2048>>>，那么2024个数据可以被2024个threads一次执行完毕，其中有24个threads空闲，因为因为没有多余的数据去处理。

如果还是2024个数据，而我的GPU只允许用户一次配置512个threads。我的kernel配置是<<<1, 512>>>，一次是不能把数据全部处理完的。当第一次处理完后，还要3次threads的id更新，最后一次有24个threads空闲，因为没有多余出具需要被处理。

kernel代码片段如下：

1
2
3
4
5

int id = threadIdx.x + blockDim.x * blockIdx.x;
while(id < N){
    // TODO excute operation
    id += blockDIm.x * gridDim.x;
}

其中while()判断当前thread的id需要更新多少次。

• 对于<<<1, 2048>>>的kernel，处理2024个数据，其中N=2024。假如其中一个thread的起始id为0，干完活后，判断0＜2024，所以这个thread的id会被跟新为2048，此时再判断2048＜2024，返回false，这个thread的工作结束。thread的id未被更新。

• 对于<<<1, 512>>>的kernel，处理2024个数据， 其中N=2024。
  仍假如有一个thread是起始id为0，判断0＜2024，执行操作。所以跟新id为512；
  判断512＜2024，执行操作，再更新id为1024；
  判断1024＜2024，执行操作，再更新id为1536；
  判断1536＜2024，执行操作，再更新id为2048；
  判断2048＜2024，返回false。该thread的工作结束。

期间这个thread的id被更新了4次，第4次更新玩后，并无操作。

Matrix Transpose 理解id更新

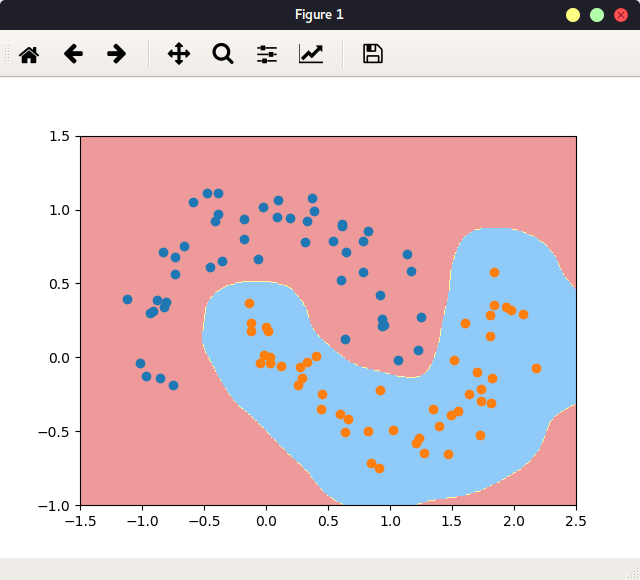
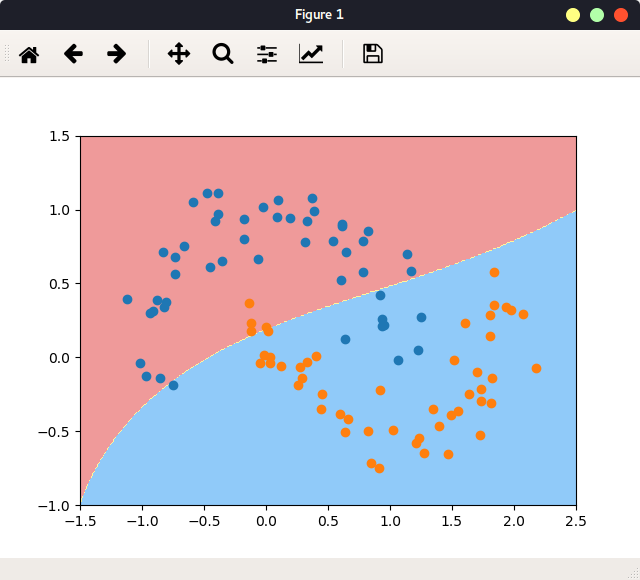
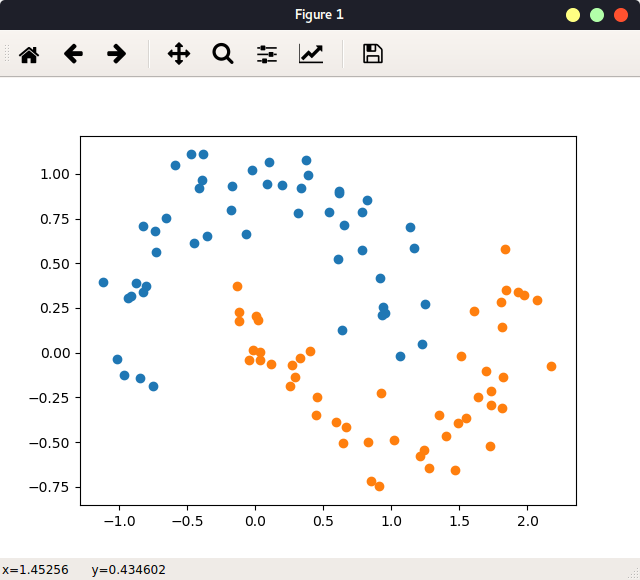
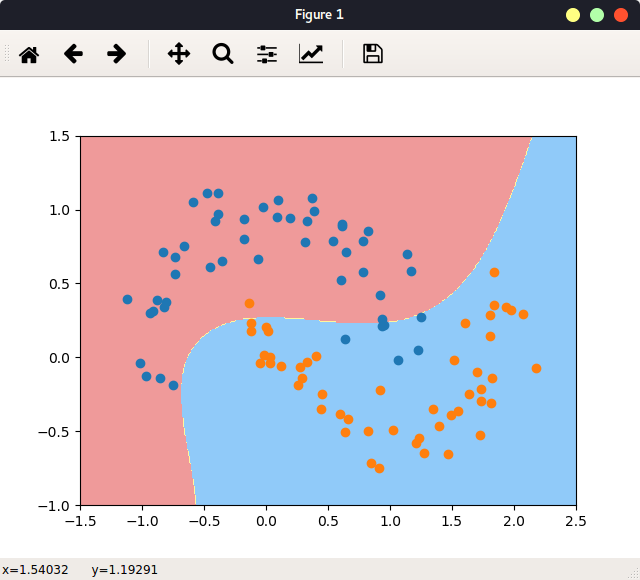
一个实例

检查环境：

• nvcc -V：CUDA编译器是否安装
• nvidia-smi：显卡驱动是否安装

cuda代码文件以.cu结尾，当写好一个文件后，使用NVIDIA 的编译器编译 nvcc FILE-NAME.cu，后./FILE-NAME执行。

从一个实例讲起：
两个向量相加，结果存入另一个向量。
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

#include <stdio.h>
#define N 1<<10  
#define ARRAY_BYTES N*sizeof(float)

// 1) add __global__ to kernel, AKA device code
__global__ void add(float* x, float* y, float* z){  
	int tid = threadIdx.x + blockIdx.x * blockDim.x;
	if (tid < N){
		z[tid] = x[tid] + y[tid];
	}
}

//host code (runs on cpu)
int main(int argc, char** argv)
{
	//allocate mem on steak for a,b,c 
	float h_a[N], h_b[N], h_c[N];

	//declare pointers in gpu   
	float *dev_a, *dev_b, *dev_c;  

	//allocate mem in gpu 
	cudaMalloc((void**)&dev_a, ARRAY_BYTES);
	cudaMalloc((void**)&dev_b, ARRAY_BYTES);
	cudaMalloc((void**)&dev_c, ARRAY_BYTES);


	//initialize a, b  arrays in the host
	for (int i=0;i<N;i++){
		h_a[i] = i * 1.0f;
		h_b[i] = i * 2.0f;
	}

	//copy a, b to gpu
	cudaMemcpy(dev_a, h_a, ARRAY_BYTES, cudaMemcpyHostToDevice);
	cudaMemcpy(dev_b, h_b, ARRAY_BYTES, cudaMemcpyHostToDevice);

	//run kernel on 1M elements on the CPU
	add<<<1, 1024>>>(dev_a, dev_b, dev_c);  //one block and 1024 threads

	//copy c back from gpu
	cudaMemcpy(h_c, dev_c ,ARRAY_BYTES, cudaMemcpyDeviceToHost);
	
	//display results
	for (int i=0;i<N;i++)
		printf("%f + %f = %f \n", h_a[i], h_b[i], h_c[i]);

	//2) free memory
	cudaFree(dev_a);
	cudaFree(dev_b);
	cudaFree(dev_c);

	//new & delete go together. 
	return 0;
}

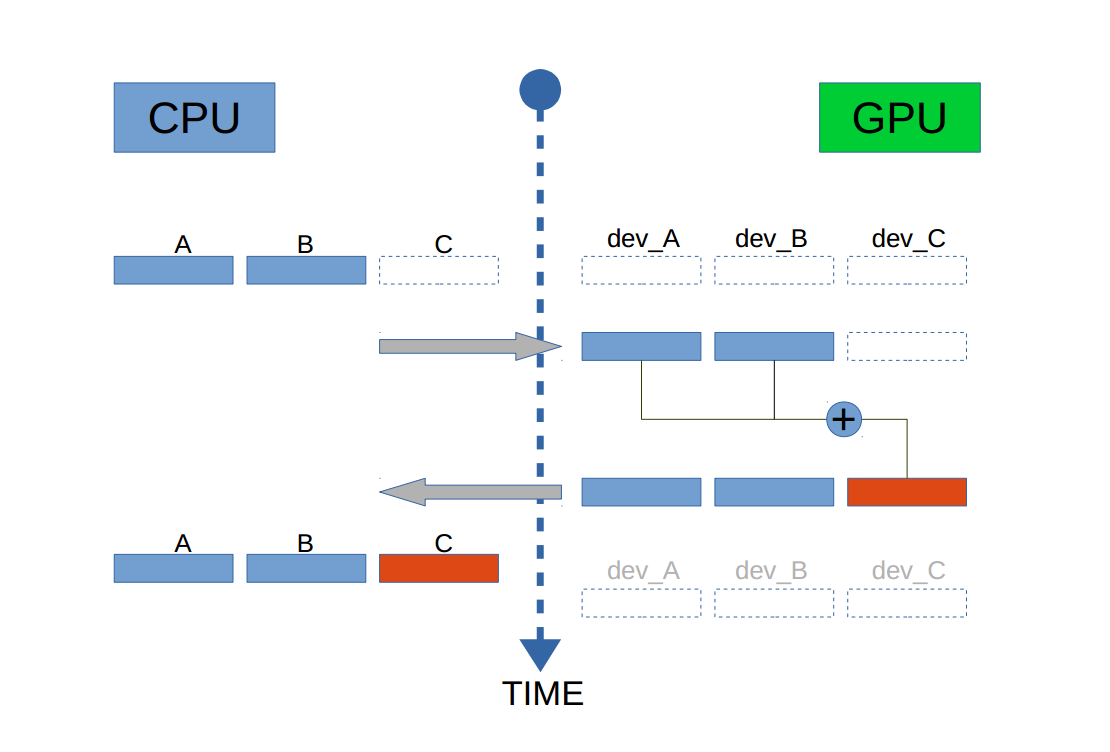
上述代码包含了CUDA代码的一般步骤：

• 1）声明所需指针在GPU，并且在GPU上开辟空间， 使用函数cudaMalloc()

• 2）从CPU拷贝所需内容到GPU的内存中，使用函数cudaMemcpy()

• 3）配置核函数，并执行操作。该函数在main函数之外，以__global__开头

• 4）把GPU上计算得到的结果拷贝回RAM，使用函数cudaMemcpy()

• 5）释放VRAM中的空间

  

从两个维度理解CUDA基本概念

• 物理层
• 逻辑层

物理概念

CUDA中的两个对象：Host，Device

• Host 包括 CPU 和内存 DRAM
• Device 包括 GPU 和存在与其上的存储 VRAM

VRAM 是 off-chip memory，即不在芯片上。由三部分组成：Global Memory，Texture Memory 和 Constant Memory。其中后二者为 read-only。
GPU 芯片上的 memory 包括 Registers，L1-cache, L2-cache 和 Shared Memory。

每个 GPU 芯片拥有一组不同的 memory，如上述。其中最重要的两个是 Global Memory 和 Shared Memory。
Global Memory 类似CPU系统的 RAM，Shared Memory 相当于CPU的片内缓存。

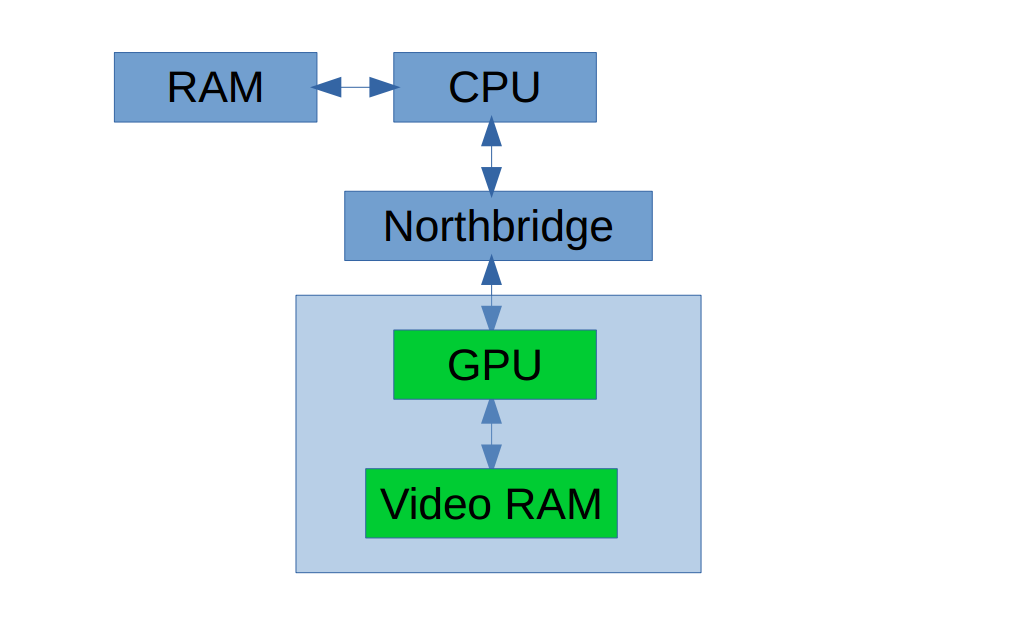
Host 和 Device 由北桥芯片连接：

对于CUDA编程，你需要负责以下内容：

1) 在 GPU memory 上开辟空间
2) 拷贝数据从CPU上到GPU上
3) 在GPU上执行 kernel 代码
4) 再把结果从GPU上考回CPU
5) 协调Host 和 Device中的操作

使用GPU编程时，要从 MIMD(Multiple Instructions Multiple Data) 的思考形式转变到 SIMD(Single Instruction Multiple Data)，在CUDA 中，每个核心执行的代码指令都是一样的，所以说是Single。

CUDA 提供的重要功能：组织线程，memory access。

与CUDA并行编程的代码分为两部分：

• Host 部分代码由 ANSI C 来完成
• Device 部分由 CUDA C 来完成，也对C++逐渐支持。

知道怎样组织 threads 在使用 CUDA 是十分重要的。

逻辑概念

在一个 grid 中所有的 thread 共享相同的 Global Memory。来自不同 block 的 threads 不能相互交流。即属于同一个 block 的 thread 可以相互交流。

• threadIdx.x: 每个 block 中 x 方向 thread 的 id
• threadIdx.y: 每个 block 中 y 方向 thread 的 id
• threadIdx.z: 每个 block 中 z 方向 thread 的 id

• blockIdx.x: 每个 block 的 x 方向上所含的 id
• blockIdx.y: 每个 block 的 y 方向上所含的 id
• blockIdx.z: 每个 block 的 z 方向上所含的 id

• blockDim.x: 每个 block 的 x 方向上所含的 thread 数
• blockDim.y: 每个 block 的 y 方向上所含的 thread 数
• blockDim.z: 每个 block 的 z 方向上所含的 thread 数

• gridDim.x: 每个 grid 的 x 方向上的 block 数
• gridDim.y: 每个 grid 的 y 方向上的 block 数
• gridDim.z: 每个 grid 的 z 方向上的 block 数

grids 和 blocks 使用 dim3 数据类型。 当给了数据的大小，如何决定 grid & block 的维度。

• 1）先决定 block 大小，即每个 block 由多少 threads，
• 2）然后根据数据大小和 block 大小，计算 grid dim。

为了得到 block dim，考虑两点：

• 1）kernel 的性能特点
• 2）GPU的物理极限
  • 我的芯片的数据：

func<<<32, 1024>>>()：

• 32：block 的数量为32个
• 1024：每一个 block 的 thread 数为1024个

为了配置 kernel 你需要知道：

• 1）kernel 的 thread 总数
• 2）这些 threads 的分布：block & grid 的维数，每个 block 由多少 threads

举例子：
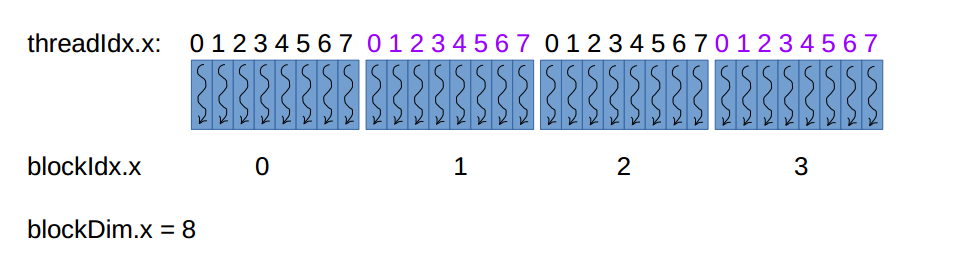
假如我想使用32个threads，我想 配置一个1D grid 1D block kernel func<<<4, 8>>>()，其 thread 分布是：

32个 threads 决定了会有32 份func()的拷贝，每一份由一个thread 执行，唯一不同的是每一个thread 的ID，这样计算：
idx=threadIdx.x + blockDim.x * blockIdx.x。
如第二个block的第一个thread 的ID是 0+8*1=8，最后一个thread的ID是7+8*3=31，所以，这个配置中的所有threads由唯一的ID：0~31。

再如：2D grid，2D block kernel：

1
2
3

dim3 threads(2, 4)
dim3 blocks(2, 4)
func<<<blocks, threads>>>

下图是所有相关的参数，及怎样得到每个 thread 的 ID：

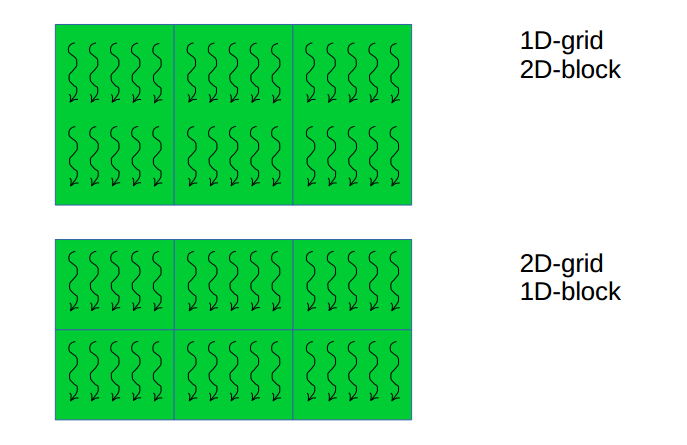
更多kernel的配置：

其中矩形表示一个block，相邻blocks组织成grid。

核心概念：
grid 由 block 组成，可以是1D，2D，和3D。
block 由 thread 组成，也可以是1D，2D，和3D。
根据具体问题，选择 block/grid 的维度。一般来说：
1D 适用于 vector 操作
2D 适用于 images
3D 适用于 3D space

杂记：

Loss Fucntion与训练

• 为啥会有Loss Function目标函数：如果要调整一个东西，让它符合一个事件的话，首先需要定义需要符合的事件是啥，这就是目标函数。也就是说，要基于什么样的目标来调整这个东西（模型）。

• 常使用的目标函数：

  • 平方差损失函数。样本标签值与预测值的距离之和
  • 交叉熵损失函数。衡量两个分布间的差距

• 训练目的：调整参数，使得模型在训练集上的损失函数值最小。

• 如何训练：直接解方程？不得行。所以有了以GD为代表的学习算法。

• 使用Mini-batch梯度下降。如果每一次都在整个数据集上计算梯度，计算量巨大，可能内存不够。如果使用随机梯度(SGD)下降，即每使用一个样本就计算一次梯度，在一个样本上得到的梯度不能反应整个数据集的梯度方向，所以收敛速度慢。所以一般使用Mini-batch梯度下降。

• 上述三种梯度下降法都存在一个缺点：会陷入局部最小值和鞍点。可以使用动量梯度下降(SGD+Momentum)。其特点是,如果当前步的方向与上一步的方向呈锐角，实际方向在二者之间，且步长较大，若是钝角，则步长小。也就是说:

  • 刚开始积累动量，加速学习。
  • 局部震荡时，梯度为0，由于动量的存在，跳出局部最优。
  • 梯度方向改变时，动量缓解震荡。

CNN

• 为啥有CNN。在传统的NN处理图像时，由于全连接，导致

  1. 计算量大

  2. 参数过多，使得过拟合

     CNN灵感来与生物的视觉感受野，其特点是局部连接，每个神经元在图片上移动时，其卷积核参数不变（参数共享），而不同的神经元间的卷积核参数不同。相比较于全连接，参数量减少了很多。参数共享：一个卷积核提取一个特征。所以CNN解决上述两个问题：

  3. 局部连接

  4. 参数共享

• 一个卷积核3通道分别与输入的3通道计算，得到的3通道计算结果相加作为输出的一个通道。如下图：

  • 即一个卷积核得到一个输出通道，所以n个卷积核得到n个输出通道。

  • 一个卷积核提取一个特征，所以6个卷积核提取6个特征。

  • 其中28 =（32-5)/1+1，即输出长=(输入长-卷积核长)/stride步长+1(步长为1)。
    

    

    注意图中的参数个数和计算量的计算与输入尺寸无关。参数计算=（核长×核宽）×（输入通道数×输出通道数）。与图中一致。

激活函数选择（添加图示）

• 线性激活函数，对于网络无效，因为是全等变换，无论网络由多少层，都相当于只有一层。我们说激活函数的作用是非线性变换，而现行变换无效果。
• 深层网络不适用sigmoid，因其计算复杂，输出均值非0，且会发生梯度消失，即更深的层参数得不到更新。
• tanh虽然输出均值为0，但计算复杂，有和sigmoid相同的问题。
• ReLU首次在AlexNet中使用，计算简单，但输出均值非0，会存在dead 神经元。
• Leaky ReLU解决了ReLU的dead 神经源问题。
• ELU输出均值接近于0，
• MaxOut是ReLU的泛华版本，没有dead神经元，但参数会翻倍。

总结：一般使用Leaky ReLU，ELU，MaxOut。

Pooling

max-pooling,average-pooling, 特点：

• 池化核移动不重叠，
• 不补零，
• 无可训练过参数，
• 作用：降采样，为下一层减少尺寸，减少计算量，减少训练参数，
• 平移鲁棒性

全连接层FC

将上一层输出展开并连接到每一个神经元上。2D变1D，没有了2D信息，所以不能再加卷基层。实际上就是普通的NN。全连接层的参数很多，一般占整个模型参数量的60%~80%。

优化算法

• SGD：

  1 2 3

  while true: dx = compute_gradient(x) x += lr * dx

• 动量SGD，解决鞍点和局部最优值，问题，每个维度的学习速率都一样：

  1 2 3 4 5

  Vx = 0 while true: dx = compute_gradient(x) Vx = rho * Vx + dx x += lr * Vx

• AdaBrad：

  1 2 3 4 5

  grad_squared = 0 while true: dx = compute_gradient(x) grad_sqaured += dx * dx # 积累平方梯度 x -= lr * dx / (np.sqrt(grad_sqaured)+1e-7)

  缺点：当learning rate较大时，分母敏感，使梯度爆炸。后期分母变大，使更新变得很小，提前结束训练。

• RMSProp：

  1 2 3 4 5

  grad_squared = 0 while true: dx = compute_gradient(x) grad_sqaured = delay_rate * grad_sqaured + (1-delay_rate) * dx * dx # 平均平方梯度 x -= lr * dx / (np.sqrt(grad_sqaured)+1e-7)

  解决了后期训练提前结束的问题。

• Adam：

  结合了动量SGD和RMSProp优点

  1 2 3 4 5 6 7 8 9 10 11

  frst_moment = 0 scnd_moment = 0 while true: dx = compute_gradient(x) frst_moment = beta1 * frst_moment + (1-beta1) * dx scnd_moment = beta2 * scnd_moment + (1-beta2) * dx * dx # 校准 frst_unbias = frst_moment/(1-beta1**t) scnd_unbias = scnd_moment/(1-beta2**t) x -= lr * frst_unbias / (np.sqrt(scnd_unbias)+1e-7)

  使得开始训练时frst_moment和scnd_moment变大来加速训练。一般使用Adam算法，从经验来讲，beta1=0.9， beta2=0.999，lr=1e-3。

• lr自适应方法：

  1 2 3 4

  # Exponetial Decay: lr = lr * e**(-kt) # 1/t Decay: lr = lr / (1+kt)

  SGD训练时间长但效果好，不过需要好的初始化，和lr自适应，如果不能找到好的初始化和lr自适应，用Adam。如果要训练更深更复杂的网络，且要求收敛速度快，推荐使用Adam。

网络需要初始化 (添加图示)

好的初始化使训练速度快，且达到一个好的结果。多层网络不适用0来初始化。

如何判断初始化的好坏？查看初始化后各层的激活函数的分布，如果分布在一个区间内，好；如果输出集中在某个值上，不好。
一般使用均值为0方差为0.02的正态分布来初始化。
对于tanh使用Xavior初始化：

1

w = np.random.rand(channel_in, channel_out)/np.sqrt(channel_in)

对于ReLU使用He-ReLU初始化：

1

w = np.random.rand(channel_in, channel_out)/np.sqrt(channel_in/2)

其网络每一层分布都相近。

批归一化

通用的归一化方法：

• 为了使得每层激活函数的分布一致，在得到激活函数值后，把输出做归一化处理：减去均值，除以方差，使得其值分布在均值为0，方差为1 的分分布上。

• 缺点：表示在每一批上做归一化，但是，一批的分布不能反应整个数据集的分布，结果是，得到一个特征，批归一化后，这个特征不能在批不批间区分样本了，即特征无效了。

• 解决：设置alpha&beta两个参数做逆归一化：

1

数学公式 填坑

数据增强

多尺度剪裁。

Fine-Tuning

在已经训练好的网络上进行微调。使用已经微调好的模型来初始化。见Fine-tuning博客。

假如网络的超参数配置如下：

1
2
3
4
5
6
7
8
9
10
11
12

def set_default_parameters():
    return tf.contrib.training.HParams(
        embedding_size=16,
        encoded_length=50,
        num_word_threshold=20,
        num_lstm_nodes=[999, 32],    # 999
        num_lstm_layers=2,
        num_fc_nodes=555,            # 555
        batch_size=100,
        learning_rate=0.001,
        clip_lstm_grads=1.0,
    )

在构建模型图的过程中，需要对LSTM单元中的每一个门制定参数大小：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

def _generate_params_for_lstm_cell(x_size, h_size, bias_size):
    x_w = tf.get_variable('x_weights', x_size)
    h_w = tf.get_variable('h_weights', h_size)
    b = tf.get_variable('bias', bias_size, initializer=tf.constant_initializer(0.0))
    return x_w, h_w, b
# one LSTM layer
with tf.variable_scope('lstm', initializer=lstm_init):
    # all params in the lstm cell:
    with tf.variable_scope('inputs'):
        ix_w, ih_w, ib = _generate_params_for_lstm_cell(
            x_size=[hps.embedding_size, hps.num_lstm_nodes[0]],
            h_size=[hps.num_lstm_nodes[0], hps.num_lstm_nodes[0]],
            bias_size=[1, hps.num_lstm_nodes[0]]
        )
    with tf.variable_scope('outputs'):
        ox_w, oh_w, ob = _generate_params_for_lstm_cell(
            x_size=[hps.embedding_size, hps.num_lstm_nodes[0]],
            h_size=[hps.num_lstm_nodes[0], hps.num_lstm_nodes[0]],
            bias_size=[1, hps.num_lstm_nodes[0]]
        )
    with tf.variable_scope('forget'):
        fx_w, fh_w, fb = _generate_params_for_lstm_cell(
            x_size=[hps.embedding_size, hps.num_lstm_nodes[0]],
            h_size=[hps.num_lstm_nodes[0], hps.num_lstm_nodes[0]],
            bias_size=[1, hps.num_lstm_nodes[0]]
        )
    # tanh
    with tf.variable_scope('memory'):
        cx_w, ch_w, cb = _generate_params_for_lstm_cell(
            x_size=[hps.embedding_size, hps.num_lstm_nodes[0]],
            h_size=[hps.num_lstm_nodes[0], hps.num_lstm_nodes[0]],
            bias_size=[1, hps.num_lstm_nodes[0]]
        )
    state_C = tf.Variable(
        tf.zeros([batch_size, hps.num_lstm_nodes[0]]),
        trainable=False
    )
    h = tf.Variable(
        tf.zeros([batch_size, hps.num_lstm_nodes[0]]),
        trainable=False
    )

查看所有可训练的参数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

<tf.Variable 'embedding/embedding:0' shape=(50513, 16) dtype=float32_ref>
<tf.Variable 'lstm/inputs/x_weights:0' shape=(16, 999) dtype=float32_ref>
<tf.Variable 'lstm/inputs/h_weights:0' shape=(999, 999) dtype=float32_ref>
<tf.Variable 'lstm/inputs/bias:0' shape=(1, 999) dtype=float32_ref>
<tf.Variable 'lstm/outputs/x_weights:0' shape=(16, 999) dtype=float32_ref>
<tf.Variable 'lstm/outputs/h_weights:0' shape=(999, 999) dtype=float32_ref>
<tf.Variable 'lstm/outputs/bias:0' shape=(1, 999) dtype=float32_ref>
<tf.Variable 'lstm/forget/x_weights:0' shape=(16, 999) dtype=float32_ref>
<tf.Variable 'lstm/forget/h_weights:0' shape=(999, 999) dtype=float32_ref>
<tf.Variable 'lstm/forget/bias:0' shape=(1, 999) dtype=float32_ref>
<tf.Variable 'lstm/memory/x_weights:0' shape=(16, 999) dtype=float32_ref>
<tf.Variable 'lstm/memory/h_weights:0' shape=(999, 999) dtype=float32_ref>
<tf.Variable 'lstm/memory/bias:0' shape=(1, 999) dtype=float32_ref>
<tf.Variable 'fc/fc1/kernel:0' shape=(999, 555) dtype=float32_ref>
<tf.Variable 'fc/fc1/bias:0' shape=(555,) dtype=float32_ref>
<tf.Variable 'fc/fc2/kernel:0' shape=(555, 10) dtype=float32_ref>
<tf.Variable 'fc/fc2/bias:0' shape=(10,) dtype=float32_ref>

可以看出LSTM单元中每一个部件的参数大小。模型中只有一层LSTM，所有的LSTM层中的999，均指的是该层有999个LSTM单元。完整实现看这里。

结合colah的这篇文章进一步理解。