GPU系统中的各种内存数量约束了整个系统中的block数量和threads数量。每个thread使用各种存储的多少影响着可以使用threads的数量。

SM资源分割:

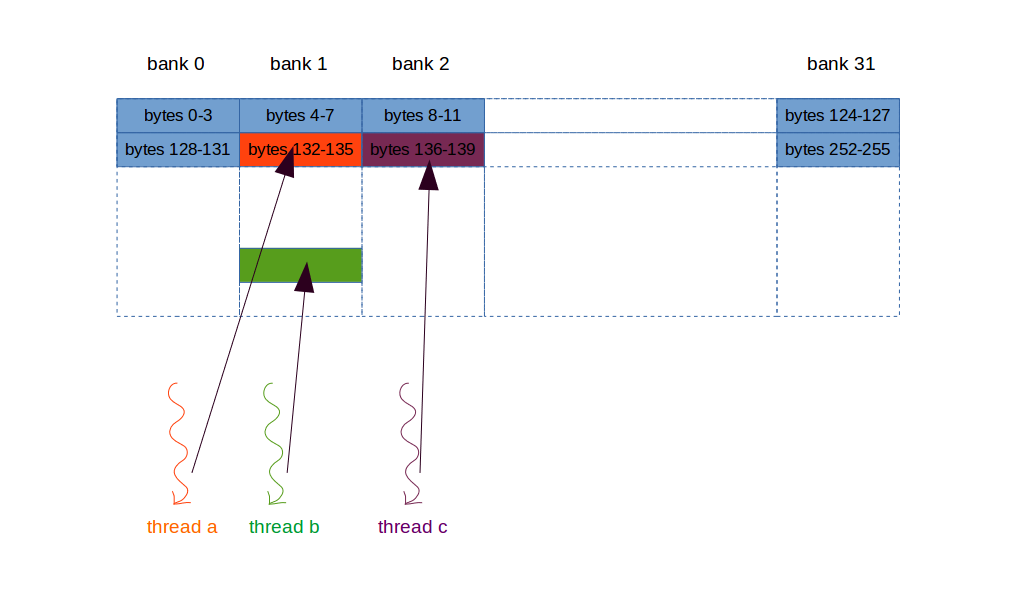
GPU的计算资源以SM为单位，SM之间共享global memory，不过通常global memory足够大，所以每个thread不管使用多少global memory，对可调用的threads数量几乎没有影响（本来设计kernel的原则之一就是最少的使用Global memory）。

增加资源占量后（thread占用Registers的数量或block占用Shared memory的数量）导致并行性急剧下降，例如，增加每个thread的register数量，可以并行的block数量就可能大幅度下降（下降是以一个block为单位下降的）。使用CUDA Occupancy Calculator工具可以修改某一资源的数值，得到其他资源的相应变化。

1. 一个SM中的Registers数量是有限的

   这些寄存器要被划分给这个SM中的所有threads。所以如果每个thread使用的寄存器过多时，这个SM中实际使用的threads数会减少，使得资源（应用程序对GPU处理单元）占用率下降。

   比如一个SM中有768个threads，含有8k个registers。要想最大并行化（最大化占用率），即使用所有的threads，那么就要保证每个thread分配最多10个registers，这种情况下共使用10x768=7680个registers，没有超过8k个。

   但是如果每个threads分配11个registers，此时11x768=8448个registers，此时算数上最多只能使用727个threads（8000/11=727.27），实际情况会比727还要少，因为超出限制后，threads数的减少是以block为粒度的减少：如果一个block有256个threads，那么可用threads数就不是从768减少到727，而是从768减少到512，只要threads数减少，就以block为单位（粒度）地减少。如果要减少threads超过256（一个block的threads数），如257，那么实际就要减少2个block（256+1，2个blocks）。

   分析一个资源分配的例子：一个SM有768个threads，8000个registers。如果每个threads使用11个registers，并且每个block含有256个threads。（上面计算过：最大并行化的register的分配是每个thread使用10个registers。）

   • 一个SM驻扎的threads个数有多少

     可用threads个数：8000/11=727个threads，而且2x256=512，3x256=768超过了727，所以这个SM驻扎2个blocks（512threads，与上述相符合）。

   • 一个SM驻扎的warp数量有多少

     2个blocks共有512个threads，所以512/32=16个warps，这个SM驻扎16个warps。而理论极限是驻扎768/32=24个warps。16远小于24.

   • warp数量减少意味着什么

     通过上述计算，没有合理分配registers的结果是，存在资源的浪费，不能最大并行化。

2. 同样的，一个SM中的shared memory的大小也是有限的

   回忆：在同一个block的threads共享同一块shared memory。

   一个SM中实际使用的block数量也是与每个block被分配的shared memory的大小有关。

   比如：一个SM有8个blocks，可使用shared memory为16kB。所以想要充分使用所有的blocks，每个block被分配shared memory最多为2kB（16kB/8）. 换句话说，为了最大并行化，充分使用SM的计算资源，这个SM中每个block可使用的shared memory最多为2kB。

   假如，每个block使用了4kB，则实际只是用了4个（16kB/4kB）blocks，相较于上一种中情况只是用了一半的threads。

   假如，每个block使用5kB，则实际只用了3个（16kB/5kB）blocks，此种情况可使用的threads就更少了。

回忆实战中，有一回，对kernel的配置没有超过硬件极限，但是实际上每个block只能使用256个threads，超过256，程序就不会得到正确结果。当时不清楚为什么，通过这篇笔记，可以解释了。是因为每个threads使用了过多的Registers（当时程序中没有使用Shared memory）的原因。导致可用threads数减少。

敲黑板Registers数量和每个block分配到的shared memory的大小，共同约束了整个系统中的block数量个threads数量。实际应用中也要尽量少的使用存储资源，从而最大化并行程度。内存是竞争资源

在Windows中不能直接使用gcc，g++编译器，即使使用CLion，也同样需要配置toolchain。除了使用Virtual Studio 之外，还有相对轻量级的工具，比如MinGW 和 Cygwin。

• 安装cmake

  并且把其安装目录的bin目录添加到系统路径中。

  安装CMake后，CMake Documentation存在于安装目录中。其中，阅读CMake Tutorial，里边有CMake的使用细节。或者阅读在线文档。

• 安装MinGW

  从这里 https://sourceforge.net/projects/mingw-w64/files/Toolchains%20targetting%20Win64/Personal%20Builds/mingw-builds/8.1.0/threads-posix/seh/
  直接下载，免安装。解压到某个位置，进入bin目录，可以看到gcc.exe 和 g++.exe。等其他组件。

  将这个bin目录的路径加入到系统环境变量中。

  额外一步：进入mingw的bin目录，找到mingw32-make.exe，将其复制一份并且重命名为make.exe。如此便可以使用make命令代替mingw32-make了，

• vim

  如果习惯使用vim，安装vim后，也要将其bin目录加入到环境变量。

• 重启机器使生效

• 测试

  在命令行中：

  1 2 3 4 5

  cmake --version g++ --version gcc --version mingw32-make --version vim --version

  应该返回正确内容。

• 使用

  创建project，编辑CMakeFiles.txt。project结构与在Linux下使用cmake是一样的。

  1 2 3 4

  mkdir test cd test vim main.cpp vim CMakeFiles.txt

  编译执行：

  1 2 3 4 5

  mkdir build cd build cmake -G "MinGW Makefiles" .. make .\test.exe

  其中cmake如果报错，将目录下的已存在的CMakeCache.txt删去，从新执行即可。
  应该可以返回期望结果。

高优先级：

• 为最大化开发者的效率，使用程序分析工具来找到程序最耗时的部分，找到效率瓶颈。

• 最大化地利用CUDA， 首先想办法把原程序中的串行代码并行化。

• 使用程序使用的有效带宽最为测量性能和优化效果的指标。

  • 理论带宽

    理论带宽可以从硬件的商品指标计算得到。比如NVIDIA Tesla V100 使用 HBM2 (double data rate) RAM 时钟频率是 877 MHz。存储器位宽为 4096-bit-wide。

    通过上述指标可以计算这个显卡的理论带宽：

    ( 0.877 × 10^9 × ( 4096 / 8 ) × 2 ) ÷ 10^9 = 898 ⁢ GB/s ⁡

    (0.877 × 10^9)表示把时钟频率转化成Hz。 (4096 / 8) × 2)将位宽单位转化成字节， 后乘以2，由于RAM是double data rate。最后除以 10^9 将最终单位转化为GB/s。

  • 实际带宽

    实际带宽通过程序的实际执行，通过下面的公式得到：

    实际带宽 = ( ( Br + Bw ) ÷ 10^9 ) ÷ time

    结果的单位是GB/s。Br表示每个kernel读取的字节数，Bw表示每个kernel写入的字节数。

    比如，一个程序要计算一个2048*2048的矩阵拷贝，整个过程的带宽：

    实际带宽 = ( ( 2048^2 × 4 × 2 ) ÷ 10^9 ) ÷ time

    其中乘以4 表示矩阵每个元素的类型是float（4字节）， 乘以2是因为由读写两个过程。最后除以 10^9 将最终单位转化为GB/s。

• 尽可能不使用PCIe，步进行Device和Host间的数据传输。数据传输很可能抵消掉并行带来的 性能提升。

  中间数据应在Device内存中创建，销毁，由设备操作。此外，由于与每个传输相关联的开销，将许多小的传输批处理为一个较大的传输要比分别进行每个传输好得多。

  此外，当使用pinned memory时，Device和Host间的带宽更高。

• 尽可能确保Global memory的访问时，地址是连续的。记住，连续的threads访问连续的地址，效率是最高的。

• 尽量少用Global memory，尽量多的使用Shared memory。

  内存指令（Memory instructions）包括读取或写入shared，local或Global内存的任何指令。当访问未缓存的local或Global内存时，内存延迟有数百个时钟周期。

  下边这个例子，的赋值运算符，有很高的吞吐量，但是从Global的读操作，会有上百个时钟周期的延迟。

  1 2 3

  __shared__ float shared[32]; __device__ float device[32]; shared[threadIdx.x] = device[threadIdx.x];

  如果在等待Global内存访问完成的同时，可以发出足够的独立算术指令，则线程调度程序（thread scheduler）可以隐藏大部分全局内存延迟。但是，最好尽可能避免访问全局内存。这种操作称为Overlap

  总之，能不用Global memory就尽量不使用。

• 在一个warp中，避免出现分支，就是说，避免Divergence。

中优先级

• 使用Shared内存以避免从Global内存进行冗余传输。见使用Shared memory对矩阵相乘进行的优化。

• 为每个线程保持足够的寄存器占用率。CUDA有个工具来计算资源占用率：CUDA Occupancy Calculator

• 对于kernel的配置，每个block中的线程数应该是32 的倍数，CUDA中32是个特别的数字，一个warp由32 个线程，Shared memory被划分成32个banks。

• 在loop中，对于循环计数器，由于循环计数器的值通常都是正的，因此可能会尝试将其声明为无符号的。但是，为了获得更好的性能，应该将它们声明为signed。

• 当速度超过精度时，使用快速的数学库。

  CUDA支持两种数学库，两种数学库通过名字区分：__functionName()和functionName()。

  • __functionName()运算时，直接映射到硬件层。快，但是精度低。
  • functionName()慢，但是精度高。

• 尽可能的使用更快，更专的数学库，而不是更慢，更通用的数学库。 这里

低优先级

• Use zero-copy operations on integrated GPUs for CUDA Toolkit version 2.2 and later.

• 使用移位运算来避免昂贵的出发和取模运算。

  Integer division and modulo operations are particularly costly and should be avoided or replaced with bitwise operations whenever possible: If n is a power of 2, ( i / n ) is equivalent to ( i ≫ log2 n ) and ( i % n ) is equivalent to ( i & n - 1 ).

• 避免将双精度数自动转换为浮点数。

  The compiler must on occasion insert conversion instructions, introducing additional execution cycles. This is the case for:

  • Functions operating on char or short whose operands generally need to be converted to an int

  • Double-precision floating-point constants (defined without any type suffix) used as input to single-precision floating-point computations

    The latter case can be avoided by using single-precision floating-point constants, defined with an f suffix such as 3.141592653589793f, 1.0f, 0.5f.

    For single-precision code, use of the float type and the single-precision math functions are highly recommended.

    It should also be noted that the CUDA math library’s complementary error function, erfcf(), is particularly fast with full single-precision accuracy.

• 让编译器很容易使用分支预测代替（in lieu of）循环或控制语句。

  Sometimes, the compiler may 循环展开 unroll loops or optimize out if or switch statements by using branch predication instead. In these cases, no warp can ever diverge. The programmer can also control loop unrolling using #pragma unroll.

Local Memory

Local memory 的命周期是一个thread，它存在与Global memory中，所以对Local memory的访存是低效的。

Local memory 是存储自动变量的。通常自动变量是较复杂的structures 或者数组，这些对象都会消耗太多的这个线程的寄存器。当nvcc编译器发现没有足够的寄存器空间来保存变量时，就会将变量放进Local memory中。

有个技巧，如果一个kernel函数中需要使用数组，而且数组的长度是固定的，为了避免使用Local memory，将这个数组拆成单个的变量，这些变量会被存储到Registers中（当然是当Registers的个数足够时）。

Constant Memory

在Device中共有64KB大小的Constant memory，只读。

如果一个warp中的所有threads访问同一个Constant memory地址时，此时的访存可以和Registers一样快。所以对于只读的全局数据，选择放在Constant memory中。

Registers

通常，访问寄存器每一条指令都不会消耗额外的时钟周期，但由于寄存器的读写依赖关系和寄存器内存bank冲突，可能会出现延迟。

编译器和硬件线程调度程序将尽可能优化调度指令，以避免寄存器bank冲突。应用程序无法直接控制这些银行冲突。这些开发者不受控制。

当没有足够的寄存器可用分配给指定任务时，就会出现寄存器压力。尽管每个多处理器都包含数千个32位寄存器但它们都是在并发线程之间分配的。为了防止编译器分配太多寄存器，使用-maxrregcount=N编译器命令行选项（nvcc）或启动边界内核定义限定符来控制每个线程分配的寄存器的最大数量。

L1/L2 Cache

每个SM有自己独有的一片存储空间，这个空间被Shared memory和L1 缓存公用。而L2缓存 被所有SM公用，L2中缓存来自Global Memory中的数据。

SP访存时，先从L1中找数据，若没有则从L2中找，若仍没有，从Global Memory中找。

线程连续访问（Coalesced Access）的好处，是所需的数据很可能已经缓存在L2上，cache hit，此时的访问速度很快。回顾卷积的例子。

Allocation

使用cudaMallo() 和cudaFree()在Device上申请, 和回收空间是很耗时的操作，所以程序应该尽可能重复利用已分配好的空间。

Shared Memory

Shared Memory 的特点：

• 与L1 cache 一起占据相同的物理空间
• on-chip
• 高带宽，低延时，相较于local 和 global memory
• 在线程间没有bank冲突
• 线程可通过shared memory 来进行协作。

Shared Memory 的快速访问。通常将经常要访问的数据，和计算中间结果放入shared memory，来减少访存的次数Shared Memory。

为了在并发访问中，实现高的内存带宽，shared memory被分成大小相等的块，banks，这些banks可以被同时访问。所以任何对n个不同banks进行访存，这些访存是同时的。这就实现了高带宽。

再深入一点，shared memory 被划分为banks，一个bank对外有一个接口，使得每个周期只相应这个bank中的一个地址。所以对于同一个bank的不同地址的并发访问将导致bank conflict。如下图中的threads a和threads b，同时访问bank 1，冲突了。冲突了怎么办，冲突的访存会被排队串行执行。

这就是shared memory 架构的设计特点。看更详细的bank，看这里。

关于bank conflict：

• 一个Warp中的所有（多个）threads访问不同的banks，无冲突。如图中thread c与thread a不冲突，thread c与thread b也不冲突。

• 一个Warp中所有（多个）的threads访问同一个地址，这是广播，无冲突。这个地址所在的bank只相应这个地址，所以可以同时访问。[In this case, multiple broadcasts from different banks are coalesced into a single multicast from the requested shared memory locations to the threads. ]

• 关于bank conflict，一个Warp有32个threads，一个bank中的地址也是32，所以bank conflicts 可能发生在同一个warp中的任何线程。

读书笔记来自这里

APOD

• APOD 表示Assess，Parallelize, Optimize, Deploy。是Nvidia官方提出的CUDA应用程序的周期性设计模式，目的很明确，让开发者快速找到程序中可以并行的部分，尽可能地加速计算。

  1. Assess 作为循环设计的入口，评估程序中最耗时的代码部分。

  2. Parallelize 根据原始代码，调用现有的GPU优化库（如cuBLAS，cuFFT或Thrust），也可以简单地添加一些预处理器指令作为并行化编译器的提示。

  3. Optimize 有很多方法，可以从很多角度，比如 overlapping data transfers， fine-tuning floating-point operation sequences 等等。这一步一定要用可用的优化工具。

  4. Deploy 经过初步优化后，保证正确性，在有限时间内得到一个较好的结果。而不是将所有可能优化都实现。

     根据具体任务和产品，迭代4步骤。尽可能的得到好的性能提升。

• 建立优化优先级

  在执行优化前要建立优化优先级。

  高优化优先级是一些优化，这些优化对于大部分CUDA程序而言可以显著提升性能。低优化优先级是一些小的优化，这些优化可能只适用于某些特定的情况下。

  先处理高优先级的优化，后解决低优先级的优化。这保证了在有限时间内提供足有的结果，并且避免了过早优化（premature optimization）。

  常见高优先级：

  1. 用profiler工具找到最耗时的部分
  2. 并行处理可以并行的串行部分

Host 和 Device 的不同

同时含有CPU和GPU的计算系统称作是异构计算系统（Heterogeneous Computing）。为了有效是哟个CUDA，有必要知道Host和Device 的不同。

• 线程资源

  Host上的流水线可以支持有限数量的并发线程。比如，具有2个32核芯处理器的服务器只能同时运行64个线程（如果CPU支持同时多线程，那么可同时运行的线程数为64的倍数，如128，192）。

  相比之下，CUDA设备上最基本的并行执行单元包含32个线程（一个warp）。现代NVIDIA GPU可以在多处理器上同时支持最多2048个活动线程。如果一个GPU上有80个多处理器（SM），这表示可以有超过160000个并发活动线程。

• 线程本身

  CPU上的线程通常是重量级实体。操作系统必须用其他线程交换CPU执行通道上的线程，以提供多线程功能。因此，上下文切换（当两个线程被交换时）是缓慢而昂贵的。

  相比之下，GPU上的线程是轻量级。在一个典型的系统中，数千个线程排队等待工作。如果GPU要等待一个warp，它只需在另一个warp上开始执行工作。因为单独的寄存器被分配给所有活动线程，所以在GPU线程之间切换时不需要交换寄存器或其他状态。资源一直分配给每个线程，直到它完成执行。

  简而言之，CPU内核目的是最小化每次一小部分线程的等待时间，而GPU则被设计成处理大量并发、轻量级线程以最大化吞吐量。

• RAM

  Host由CPU和系统内存构成，Device由GPU和显卡上的存储器构成。所以说，Host和Device有各自的RAM。

这些是硬件层面就并行角度看的不同。总之在这样的异构系统中Host做串行工作，Device做并行工作。

Profiling

目的是找到程序中最耗时函数。有很多Profiler工具，比如gprof：

1
2
3
4
5
6
7
8
9
10
11
12
13

$ gcc -O2 -g -pg myprog.c
$ gprof ./a.out > profile.txt
Each sample counts as 0.01 seconds.
  %   cumulative   self              self     total           
 time   seconds   seconds    calls  ms/call  ms/call  name    
 33.34      0.02     0.02     7208     0.00     0.00  genTimeStep
 16.67      0.03     0.01      240     0.04     0.12  calcStats
 16.67      0.04     0.01        8     1.25     1.25  calcSummaryData
 16.67      0.05     0.01        7     1.43     1.43  write
 16.67      0.06     0.01                             mcount
  0.00      0.06     0.00      236     0.00     0.00  tzset
  0.00      0.06     0.00      192     0.00     0.00  tolower
  ...

其中genTimeStep函数是最耗时的。所以是我们优化对象

Strong Scaling & Weak Scaling

这是两类不同的问题，还有两者的混合问题。

了解这里的目的是啥，是为我们的加速设置一个期望值，并且计划一个增强并行化的策略。

1. Strong scaling 表示待解决的问题总体大小是固定的，当使用更多的处理单元时，解决该问题的时间会相应地减少。

   对应的测量加速公式是Amdahl's Law。

2. Weak scaling 表示每个处理单元（处理器）内所解决的问题大小是固定的，随着处理器数量的增加，问题的总量也会变大。

   对应测量加速的公式是Gustafson's Law。

公式理解看这里

得到正确结果是所有计算的目的

一个并行系统可能遇到的关于结果正确性的问题，这些问题在一个串行系统中是不存在的：线程问题，浮点计算带来的问题，CPU和GPU的不同计算方式带来的问题。

为什么出现计算机。计算机是发展出来的。从电子管到晶体管到集成电路到超大规模集成电路，到未来的生物计算机，量子计算机。

早期计算机只含有固定用途的程序，这导致了，如果要改变工作内容，即程序，就需要重新设计结构电路。在没有通用计算机的当时，重新设计电路就很低效率。所以有了冯诺依曼的思想：

把程序存储起来，并且设计通用电路。当需要运行某个程序时，将程序和数据放入存储器中，把程序翻译成电路能理解的语言，让通用电路执行逻辑。这就是冯诺依曼思想的核心 “存储程序指令，设计通用电路”。

所以可以总结冯诺依曼体系是将程序指令和数据一起放入存储器的计算机设计概念。也就是说，用户只需要输入不同的程序被数据，就可以改变计算机的操作。

具体说就是，创造通用的指令集结构，将程序转化成一串指令的集合。指令作为一种特殊的静态数据，这使得一台计算机可以改变运行内容，而不用重新设计电路。

这是冯诺依曼的贡献。

冯诺依曼体系的基本组件：

1. 存储器。存储运行时的程序和数据
2. 程序计数器PC。执行到哪一步，下一步执行什么。能长期记忆程序数据中间结果以及最终结果
3. 运算器。具备算术，逻辑运算和数据传送等数据加工处理能力
4. I/O设备。能把所需程序和数据，传送至计算机中。能将计算结果传入，输出给用户

冯诺依曼体系的瓶颈：CPU和存储器速率之间的问题无法调和，CPU运算快，存储器速度慢。

所以有了现代计算机体系架构。但也是在冯诺依曼体系上改进的。为了解决上述瓶颈，将存储器加入到CPU中组成了现代的CPU。

所以现代计算机架构的核心，是以存储器。

查看所连接WiFi及psswrd

1. 查看所有链接过的WiFi：

   $ cd /etc/NetworkManager/system-connections
$ ls

2. 选择所查看WiFi,显示配置文件：

   $ sudo vim TP-LINK_DBBB

3. 对应密码在wifi-security字段的psk处

为应用创建快捷方式 如firefox

1. 下载firefox

2. $ tar -xvf firefox-70.0.1.tar.bz2 解压

3. $ mv firefox /opt 将解压后文件放入opt

4. $ cd /usr/share/applications

5. $ sudo touch firefox.desktop 创建桌面图标文件

6. $ sudo vim firefox.desktop 编辑文件

   [Desktop Entry]
   Name=Firefox
   Comment=this is firefox
   Exec=/opt/firefox/firefox
   Icon=/opt/firefox/chrome/default/icons/default128.png
   Terminal=false
   Type=Application
   Categories=Application;Network;

   Exec是Firefox可执行文件的路径；Icon是Firefox应用图标路径

7. icon加入了application 列表，便可以快速访问了

apt install fail

Linux 中sudo apt install ...时关于could not get lock /var/lib/dpkg/lock -open(11:Resource temorarily unavailable)的解决方案：

• 第一步：找到所有含有“apt”的进程：

  $ ps -A | grep apt

• 第二步：删除所有你含”apt”的进程：

  $ sudo kill -9 进程ID

更新activation key(windows)

• 卸载之前的key

  > slmgr.vbs /upk

• 安装新的key

  > slmgr /ipk XXXXX-XXXXX-XXXXX-XXXXX-XXXXX

• 设置计算机秘钥管理地址

  > slmgr /XXX.XXX.XXX

• 激活

  > slmgr /ato

修复U盘（Windows）

当优盘出现问题时，比如作为系统盘使用后的异常。可以使用一下方法修复。windows中。

在terminal中依次输入下面命令：

1. diskpart: 进入磁盘交互界面

2. list disk: 返回机器中的所有磁盘的列表。比如“磁盘0”，“磁盘1”.

3. select disk 1: 选择待处理的盘，比如“磁盘1”，从容量上也可以区分。

4. clean: 删除U盘下的所有分区。

5. create partition primiry: 在U盘中建立一个主分区。

6. active: 激活

7. format fs=fat32 quick: 快速格式化磁盘为fat32格式。加quick与没有加quick的区别：

   • 加quick只是删除磁盘中的文件。
   • 不加quick是真正地格式化，将磁盘重新分道分簇。

8. exit: 推出磁盘交互界面

Windows系统用户临时文件

定期将用户临时文件删除。

系统盘->用户->自己的账户->显示隐藏那个文件->AppData。AppData中有三个文件夹：

1
2
3

├── Local
├── LocalLow
└── Roaming

这三个文件夹中的Temp文件夹都是用户临时文件，删。

记录两种看待矩阵的重要视角，对于推理, 证明和理解线性代数其他概念都十分重要。

• 列向量 坐标系或空间
• 行向量 函数或线性方程组

列视角

两矩阵相乘，将左边的方阵A看做是坐标系或空间，右边的矩阵B是一个列向量的集合，每一个列向量表示在空间A的表式，而相乘的结果是在这个维度的空间中的标准正交基下的同一个列向量的表示。如

看个例子：

把矩阵A看做是由列向量构成的，a，b 是两个列向量经过A变换得到的结果。c 是将两个列向量放在一起，构成了矩阵B，矩阵B中每个列向量经过A变换的结果。

结果是相同的。向量trans([2,3]) 是向量trans([7,7])在空间A中的表达，

行视角

还可以将A看作是一个函数或线性方程组. 右边的向量或矩阵是操作对象。

看个例子：

把矩阵A看做是由行向量构成，e，f 是分别操作两个列向量。g 是将两个列向量放到一起，一起处理。

结果相同，可以看出B中的列向量彼此间是无关的，都经过A相同的变换。

一个例子

证明矩阵对角化中一个结论：

如果可以将A分解成P*D*(P逆). 那么有D和P可以分别为：

其中lambda为A所对应的所有特征值，u是对应lambda的特征向量。(P 中的u向量竖着写)。

现在问题是，如何证明：如果D，P为上述矩阵，A有n个线性无关的特征向量，那么有：

证明A=P*D*(P逆)， 就是证明AP=PD，观察等号左右：

左右相等，证毕。

表达式i中A为一个函数，操作与右边每一个列向量。但并没有展开，因为根据特征值特征向量的定义，可以将A用lambda替换。

而表达式ii的过程，就是将左边矩阵每一列当成一个列向量考虑，实际上，这个矩阵就是由列向量构成，所以自然而然的将这个矩阵用类向量的视角看待。

当所处理的对象数值很大时，如(int)32634573563452724846734573，使用整型长整型，都会溢出，这种情况就要使用字符串代替数字。此方法处理大数问题。

两个知识点：

1. 字符型的数字与其对应的ASCII值：

   char	‘0’	‘1’	‘2’	‘3’	…	‘9’
   int	48	49	50	51	…	57

2. char与对应int转换

   char->int: '3'-'0' = 3
   int->char: 3 +'0' = '3'

问题描述

给一个n位数，打印从1到最大的n位数。比如n=3，则打印1,2,3，...，998,999.

思路

当n为20，其对应的数值已经远远超过了计算机可以表示的范围，所以用字符串表示一个大数，并且实现中不能出现for循环，因为循环变量i随循环次数也会超出表示范围的。所以用while循环避免使用循环变量。

实现

下面的实现是有冗余的，只用addOne()或subtractOne()其一即可。当使用addOne()时，只要加一后的string不等于最大的n位数，就打印，后循环；当使用subtractOne()，初始string设为最大的n位数，while循环减一，只要这个string不是空，就打印，后循环。

当然两个函数可以配合使用，不过就多余了，但就当练习大数操作了。

一个string表示的大数加一操作如下。先在string首位插入一个’0‘占位，可能加一后要进位：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

// 初始化为“0”，循环中加到最大值
string addOne(string num) {
    if (num.size() == 0) return " ";
    num.insert(0, 1, '0');

    int carry = 1;
    int i = num.size() - 1;
    while (carry != 0) {
        int sum = (num[i] - '0') + carry;
        carry = sum / 10;
        int remainder = sum % 10;
        num[i] = remainder + '0';
        i--;
    }
    return num[0]=='0' ? num.substr(1) : num;
}

一个string表示的大数减一的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

// 初始化为最大值，循环中减到空
string subtractOne(string Nine) {
    bool borrow = false;
    int length = Nine.size();
    int iter = length - 2;
    int val;
    if (Nine[length - 1] == '0') {
        borrow = true;
        val = 10 + (Nine[length - 1] - '0') - 1;
        Nine[length - 1] = val + '0';
    }
    else Nine[length - 1] = Nine[length - 1] - '0' - 1 + '0';

    while ( borrow && iter >= 0) {
        if (Nine[iter] == '0') 
            val = 10 + (Nine[iter] - '0') - 1;
        else {
            borrow = false;
            val = (Nine[iter] - '0') - 1;
        }
        Nine[iter] = val + '0';
        iter--;
    }
    return Nine[0]=='0' ? Nine.substr(1) : Nine;
}

主函数，仔细分析，上述两个操作，使用一个就可以达到目的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

void solution(int n) {
    if (n <= 0) return;

    // 最大的n位数 str
    string str;
    for (int i = 0; i < n; i++)
        str += '9';
    cout << str << endl;

    string preNum = addOne("0"); // 初始化为“0”，循环中加到最大值
    string isZero = subtractOne(str); // 初始化为最大值，循环中减到空

    while (isZero != "") {
        cout << preNum << " ";
        preNum = addOne(preNum);
        isZero = subtractOne(isZero);
    }
    cout <<str<< endl;
    return;
}

敲黑板

1. 体会subtractOne中的bool borrow = false;，表示向前借位否，
2. 实现中总会用到知识点2.

415大数相加

依然使用到上述知识点2，思路直接，实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

string addStrings(string num1, string num2) {
    int length1 = num1.size();
    int length2 = num2.size();

    if(length1 != length2){
        int diff = abs(length1-length2);
        length2 > length1 ? 
            num1.insert(0, diff, '0') :
            num2.insert(0, diff, '0');
    }
 
    int length = num1.size() + 1;
    string res(length,'0');

    int carry=0;
    for(int i=length-2; i>=0; i--){
        int sum = (num1[i]-'0') + (num2[i]-'0') + carry;
        carry = sum/10;
        int remainder = sum%10;

        res[i+1] = remainder + '0';
    }
    if (carry) res[0] = carry + '0';

    return res[0]=='0' ? res.substr(1) : res;
}