bit操作

知识点

1. 一个整数除以2，与将这个整数右移1位等价，但是移位运算效率更高。
2. 一个整数减一，后与原整数做‘与’运算，这个操作会把这个整数最右边的1变成零。

有了上述两点，求二进制中1的个数，思路就有了：

1
2
3
4
5
6
7
8

int numberOfOne(int num){
    int count = 0;
    while(num){
        count++;
        num = num & (num - 1);
    }
    return count;
}

此方法对正负整数均使用。

注意1.

• 这句话什么意思：

  1	ListNode* dhead = new ListNode(-1);

  新建一个ListNode型ptr，新建一个ListNode结点，用-1初始化这个结点的val变量，用这个ptr指向这个结点。

• 这句又是都什么意思

  1	ListNode* curr = dhead;

  新建一个ListNode型指针curr，这个指针中存储dhead中所存储的结点地址。即这两个指针类型变量所存储内容相同。就是一般赋值操作的意义了。

• 这句又是什么意思

  1	ListNode node = head;

  实例化一个ListNode，用head的val和next初始化ListNode的val和next。这个operator=是C++帮我们写好的。

所以为了不用单独处理链表的头结点，通常新建一个d_head：ListNode* d_head = new ListNode(-1);，操作过程中，d_head不应该被移动，最后就可以将他delete掉，就像上述code中的伤处操作。

注意2.删除某一个结点

1
2
3
4
5

ListNode* dNode = curr->next; //新建ptr，指向curr->next
...
...
delete dNode; // 删除指针所指向地址的内容，指针所指向地址不变。
dNode = nullptr; // 间指针设为空指针。

从链表中删除，插入结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83

#include <iostream>

using namespace std;

struct ListNode{
    int val;
    ListNode* next;
    ListNode(int x):val(x), next(NULL){}
};

// 向链表head的pre_val节点后插入val的结点。
void insertNode(ListNode* head, int val, int pre_val){
    ListNode* d_head = new ListNode(-1);
    d_head->next = head;
    while(d_head->val != pre_val){
        d_head = d_head->next;	// dhead 移动了，所以最后不能删
    }
    ListNode* insertNode = new ListNode(val);
    insertNode->next = d_head->next;
    d_head->next = insertNode;
}

// 从链表head中删除delete_val的结点
ListNode* deleteNode(ListNode* head, int delete_val){
    ListNode* dhead = new ListNode(-1); // 新建结点
    dhead->next = head;

    ListNode* curr = dhead;  //新建ptr，指向head
    while(curr->next){
        if(curr->next->val == delete_val){
            ListNode* dNode = curr->next; //新建ptr，指向curr->next
            curr->next = dNode->next;
            // 删处结点
            delete dNode;
            dNode = nullptr;
        }else
            curr=curr->next;
    }
    ListNode* resHead = dhead->next;  //新建ptr，指向dhead->next
    delete dhead;    // 整个过程dhead没有移动，所以可以delete 
    dhead = nullptr;
    return resHead;
}

// 打印当前链表
void printLinkedList(ListNode* head){	
    ListNode* node = head;
    while(node){
        cout<<node->val<<"->";
        node = node->next;
    }
    cout<<"NULL"<<endl;
    return;
}

int main(int argc, char** argv){
    // create a linkedlist
    int length, nodeVal, headVal;
    cin>>length;
    cin>>headVal;
    int count=length;
    ListNode* head = new ListNode(headVal);
    count--;
    ListNode* dhead = head;
    while(count!=0){
        cin>>nodeVal;
        ListNode* node = new ListNode(nodeVal);
        dhead->next = node;
        dhead = dhead->next;
        count--;
    }
    printLinkedList(head);
    //operations
    int insertVal;
    cin>>insertVal;
    insertNode(head, insertVal, 2);
    printLinkedList(head);
    int dln;
    cin>>dln;
    ListNode* nhead = deleteNode(head, dln);
    printLinkedList(nhead);
    return 0;
}

创建链表，打印链表，销毁链表

作为基本操作，为测试时提供便利。先在ListNode定义中中添加一个构造函数：

1
2
3
4
5
6
7

struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

传入一个保存结点值的容器，创建链表：

1
2
3
4
5
6
7
8
9
10
11
12
13

ListNode* createList(vector<int>& nodeVals){
	if (nodeVals.size()==0) 
        return nullptr;
	vector<ListNode*> nodePtr;
	nodePtr.push_back(new ListNode(nodeVals.back()));
	nodeVals.pop_back();
	while(!nodeVals.empty()){
		nodePtr.push_back(new ListNode(nodeVals.back(), nodePtr.back()));
		nodeVals.pop_back();
	}

	return nodePtr.back();
}

遍历打印链表：

1
2
3
4
5
6
7

void showList(ListNode* head){
	for (ListNode* i = head; i!=NULL; i=i->next){
		cout<<i->val<<"->";
	}
	cout<<"NULL"<<endl;
	return ;
}

销毁链表：

1
2
3
4
5
6
7
8

void destroyList(ListNode* head){
	if (head){
		destroyList(head->next);
		delete head;
        head = nullptr;
	}
	return;
}

记录Linux平台及其上常用软件的快捷键。提升效率

通用

Fn+left/right: 在文本编辑时，移动cursor与行首/行尾
ctrl+left/right: 文本编辑时，以单词为单位移动cursor
上边移动cursor时按住shift: 选中cursor走过的内容

Linux

grep -n -H -r "CUDA_KERNEL_LOOP": 在当前路径下查找所有含有此关键字的文件，并显示文件名，行号。
tree -d: 显示文件夹树

Alt + F4: close current window
Alt + PrtSc: take screen shot on current window
Alt + F7: move current window
Alt + F8: use arrow to adjust the size of current window
Alt + arrows: move out or move in a directory\
Win + D : show desk

$ make clean: 清理编译内容
$ make all -j4: 使用4个线程编译
$ cp -r foldername ./: 将foldername中所有内容复制到 当期那目录
$ rm -t foldername: 删除foldername及其中所有内容.
$ systemctl suspend: suspend mode，保存当前工作内容与内存，按任意键唤醒
$ systemctl hybernate: 也是睡眠，保存当前工作内容，但要按电源键唤醒

$ sudo apt-get install -f: ?
$ sudo apt-get update: ?
$ sudo apt-get upgrade: ?

$ Libreoffice FILENAME.odt: open .odt file

$ ls | wc -l: the number of files in current path
$ ls -l | grep ^- | wc -l: the number of files in current directory
$ ls -l | grep ^d | wc -l: the number of directories in current directory

$ mv 'ls | head -1000' ../: move first 1000 files from current to upper level
$ find /opt/opencv/ -name "imgproc.hpp": find file in a directory
$ sudo dpkg -i FILENAME.deb : install .deb file
$ dpkg --list: show installed software in system
$ sudo apt-get --purge remove (name) :packages uninstall

$ df -lhT :info about disk
$ tar -zcvf 压缩包名.tar.gz 源文件: 压缩.tar.gz

$ git clone URL : GitHub url to current directory
$ git add FILENAME: 向remote添加新文件FILENAME
$ git commit -m "massage": make a commitment about that change
$ git push: 将本地的改变推入remote
$ git pull: 更新本地repository

$ ipython trust filename.ipynb: trust this notebook

$ source activate tensorflow: activate tensor environment
$ source deactivate: deactive that environment

$ which/whereis/type package: show where is that package

$ export PS1=’:> ’ change the prompt(shorten prompt when it is too long)
:> bash change back

$ xdg-open . : open the current directory in terminal
$ sudo apt-get install alacarte: 删除Linux中invalid app icon

Chrome & Firefox

Ctrl + Tab or Ctrl + PgDn: Jump to next open tab
Ctrl + Shift + Tab or Ctrl + PgUp: Jump to the previous open tab
Ctrl + t: New tab
Ctrl + w: close current tab
Ctrl + n: new windows

Terminal

ctrl + a:移动光标到头
ctrl + e:移动光标到尾
ctrl + u:删除光标所在行
ctrl + k:
ctrl + r:历史中搜索
!xxx: 调用最后一个以xxx开头的命令（当命令较长时）
export PS1="-->": 缩短命令行

Quake Terminal

ctrl+shift+t: new tab
ctrl+shift+w: close tab
ctrl+page up: go to previous tab
ctrl+page down: go to next tab

Ipython notebook (非Edit模式下)

b: add cell below
a: add cell above
1: change cell to head 1
2: change cell to head 2
Esc: change to command mode
Enter: change to edit mode
d+d: delete cell
Shift+l: show/close line numbers

Tmux

ctrl+b: pre-fix P
ctrl+b arrows: move around windows
ctrl+b %: split window l&r
ctrl+b ”: split window u&d
ctrl+b x: kill this split-screen
ctrl+b &: kill this window
kill-server : kill all sessions

For more info check here

Intellij

ctrl+shift+F7:for a specific variable, highlight them
F3: navigate among these variables.
ctrl+w: select word
Esc: quit highlights.

pycharm

ctrl+shift+-：折叠
ctrl+shift++：展开

Docker

$ Docker(rosslee:zhen0miaod):
$ sudo docker login: login my docker hub account

$ sudo docker images -a: show all downloaded images
$ sudo docker rmi <name|id>: delete downloaded image
$ sudo docker rmi $(docker images -a -q) : remove all images

$ sudo docker ps -a: list all containers
$ sudo docker rm <name|id>: remove containe

Visual studio 代码调试

1. 跟踪变量，一步一步执行

F9: 在鼠标当前位置设置breakpoint。
F5：开始debug。在菜单栏中点击degug -> Windows -> autos。如此便可以看到每个变量的值随着调试的过程动态改变。
选中code中变量，右键->add watch: 将这个变量放入跟踪中。
Continue按钮：开始执行，到下一个breakpoint
F10: 不同与continue，这个是一句一句执行，可以跟踪临时变量。但是这回跳过子函数。
F11：一句一句执行，回进入子函数。

2. run without debugging

ctrl+F5

• 假设CUDA已经成功安装，先确定CUDA的版本

  cat /usr/local/cuda/version.txt

• 进入cudnn官网，用户登录，在cudnn下载处根据Linux机器上的CUDA版本选择对应的cudnn版本

  1. 去nvidia cuDNN home page

  2. 点击下载

  3. 用户登录，完成问卷，提交

  4. 接受条款

  5. 选择与机器CUDA版本对应的cuDNN版本下载tar文件和Sample Code：

     cuDNN Library for Linux
     cuDNN Code Samples and User Guide for Ubuntu16.04 (Deb)

• 使用tar文件安装

  1. 转到tar文件所在目录

  2. 解压

     $ tar -xzvf cudnn-10.2-linux-x64-v7.6.5.32.tgz

  3. 复制文件到已安装的CUDA Toolkit目录，并且修改权限

     $ sudo cp cuda/include/cudnn.h /usr/local/cuda/include
$ sudo cp cuda/lib64/libcudnn* /usr/local/cuda/lib64
$ sudo chmod a+r /usr/local/cuda/include/cudnn.h /usr/local/cuda/lib64/libcudnn*

• 为了测试安装成功否，安装samples code和用户指南：

  $ sudo dpkg -i libcudnn7-doc_7.6.5.32-1+cuda10.2_amd64.deb

• 测试

  1. 把Samples Code 复制到可写的目录下$HOME

  2. 进入这个可写目录

     $ cd $HOME/cudnn_samples_v7/mnistCUDNN

  3. 编译 mnistCUDNN 实例

     $ make clean && make

  4. 运行可执行文件

     $ ./mnistCUDNN

     如果可以返回如下，表示安装成功：

     Test passed!

#213 House Robber II

• 描述

  1	与#198不同，这回抢的街是环形，即首位相连，依旧是在不相邻的房子间抢，求可获得的最好收益。

• 逻辑

  技巧：选择一个房子作为首：第一条街偷除第一个房子的其他房子，第二次偷除最后一个房子的其他房子。两次偷的结果取较大值。
  其中每次偷房子的方式同#198.

• 实现

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

  int rob(vector<int>& nums) { if (nums.size() == 0) return 0; if (nums.size() == 1) return nums[0]; if (nums.size() == 2) return max(nums[0], nums[1]); // 最后一间房子 不强 vector<int> memo1(nums.size(), 0); memo1[0] = nums[0]; memo1[1] = max(nums[0], nums[1]); for (int i=2; i<nums.size(); i++){ int tmp=0; for (int j=0; j<=i-2; j++) if (memo1[j]>tmp) tmp = memo1[j]; memo1[i] = max(memo1[i-1], nums[i]+tmp); } // 第一间房子 不强 vector<int> memo2(nums.size(), 0); memo2[1] = nums[1]; memo2[2] = max(nums[1], nums[2]); for (int i=3; i<nums.size(); i++){ int tmp=0; for (int j=0; j<=i-2; j++) if (memo2[j]>tmp) tmp = memo2[j]; memo2[i] = max(memo2[i-1], nums[i]+tmp); } return max( memo1[nums.size()-2], memo2[nums.size()-1]); }

#96Unique BST

• 描述

  1 2 3

  给出一个正整数n，返回从1～n可以构成不同BST 的个数。 如n=3时，可以构成的BST数量为5.

• 逻辑

  • 动手找几个n值画画图，从中找规律。

  • 状态的定义：memo[i] 表示以1～i为节点的 BST的个数。定义memo[0]=1.

  • 状态转移方程：看下示意图，以n=3为例：

    

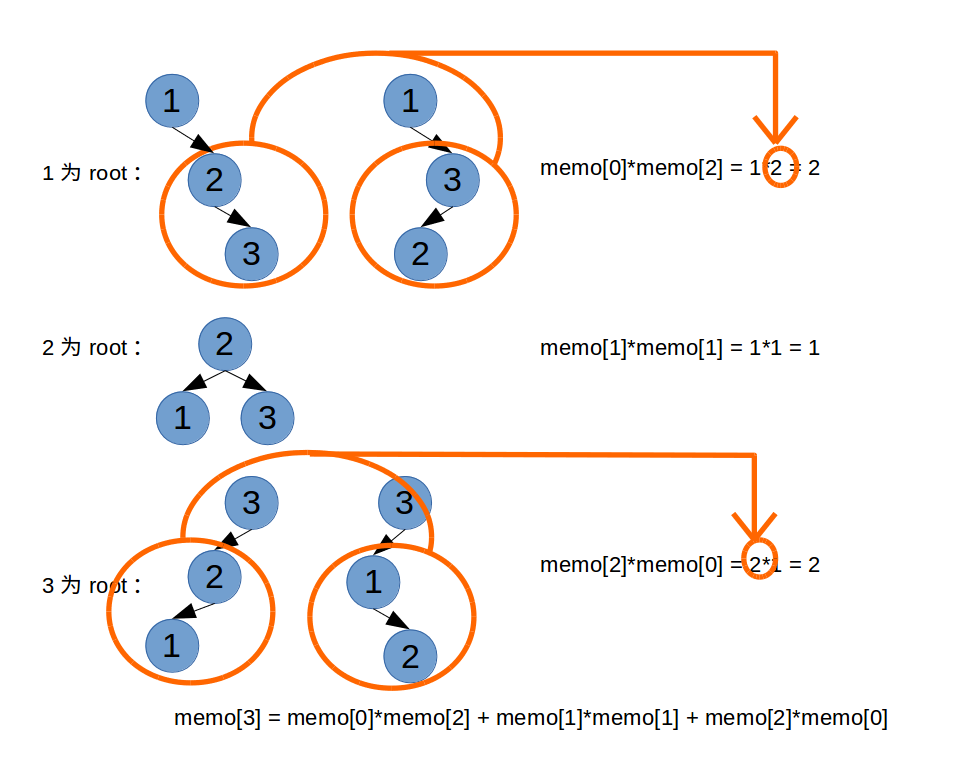
    图中memo[3]=memo[0]*memo[2] + memo[1]*memo[1] + memo[2]*memo[0] 就是n=3时的状态转移方程。

    这其中memo[2]=memo[0]*memo[1] + memo[1]*memo[0]=2 是n=2时的状态转移方程。

  • 当n=4：

    memo[0]=1;
    memo[1]=memo[0]*memo[0]=1;
    memo[2]=memo[0]*memo[1] + memo[1]*memo[0]=2;
    memo[3]=memo[0]*memo[2] + memo[1]*memo[1] + memo[2]*memo[0]=5;
    memo[4]=memo[0]*memo[3] + memo[1]*memo[2] + memo[2]*memo[1] + memo[3]*memo[0]=14;

    可以观察出，要想求出memo[1],需要求出memo[0]，要想求出memo[2],需要求出memo[1]和memo[0]...。

• 实现

  1 2 3 4 5 6 7 8 9 10

  int numTree(int n){ vector<int> memo(n+1, 0); memo[0] = 1; for (int i=1; i<=n ;i++){ for (int k=1; k<=i; k++){ memo[i] += memo[k-1] * memo[i-1-(k-1)]; } } return memo[n]; }

关键：找规律，

#304 Sum of Region

• 描述

  1 2 3 4

  给定一个矩阵，和两个点, 左上角(r1,c1)和右下角(r2,c2)。 求出由这两个点围成的矩阵所有元素之和。 NOTE，对于同一个矩阵，需要大量的上述query操作。

• 逻辑

  • 第一步：构建memo

    • 状态定义：memo[i][j]表示从matrix最左上角到matrix[i][j]处的元素之和。

    • 状态转移方程 看下图示，假如matrix如作图所示：

      

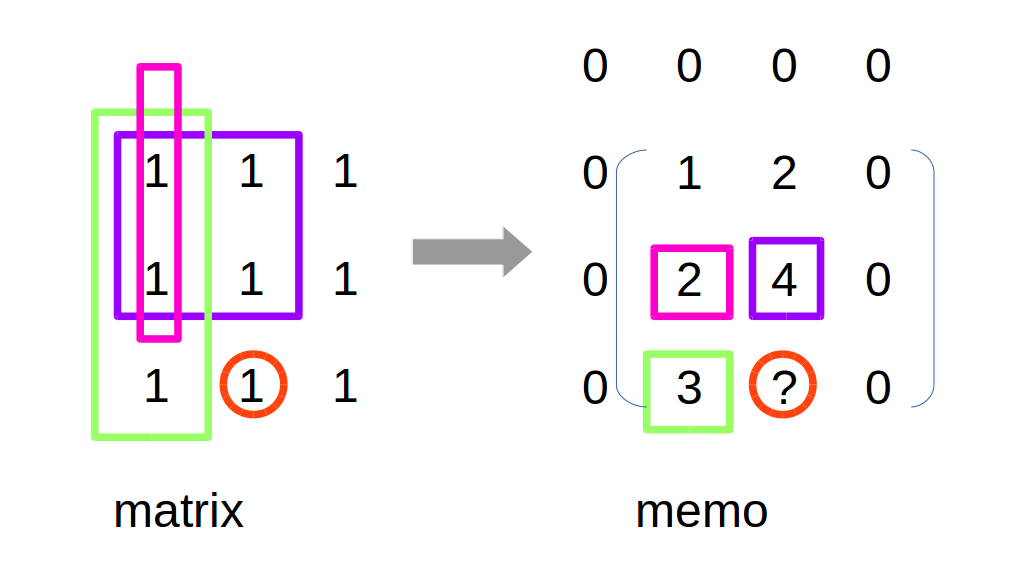
      memo中的红圈重点值如何得到? 红圈中的值按照定义，等于matrix最左上角到红圈的元素和，从作图中看就是6，怎么算的？ 6=绿+紫-粉+自身。在右图中就等于绿+紫-粉+1=6。

      所以状态转移方程是：
      当前memo值=左边memo值+上边memo值+当前matrix值-左上memo值。

      在实现中， 由于要对memo第一行和memo第一列做同样的操作，所以memo大小较matrix多了一行一列。

  • 第二步：query 从memo中取所需值。

    过程如下图：注意根据memo的定义，在matrix中的矩形，一定是从matrix最左上角开始。

    

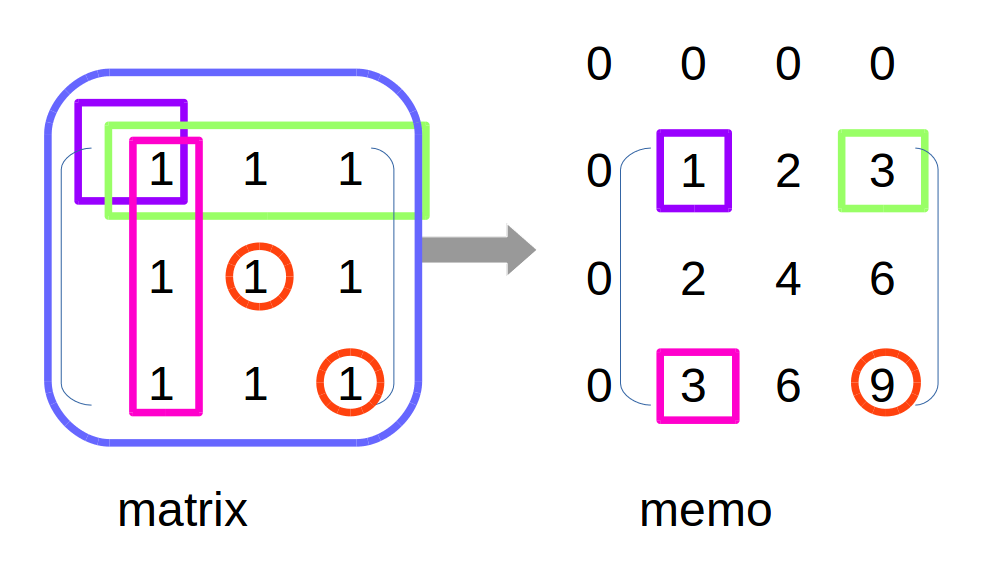
    如上图所示，假如要得到matrix中(1,1)到(2,2)元素和，在左边matrix矩阵中，就等于蓝-粉-绿+紫，对应于有图memo中就是红-粉-绿+紫。就是最终返回值。

• 实现

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  class NumMatrix{ private: vector<vector<int>> memo; public: // 构建memo数组 NumMatrix(vector<vector<int>>& matrix) { if (matrix.size()==0 || matrix[0].size()==0) return; // 在原先matrix大小基础上增加一行一列，并且初始化为0 memo = vector<vector<int>>(matrix.size()+1, vector<int>(matrix[0].size()+1, 0)); for (int r=0; r<matrix.size(); r++){ for (int c=0; c<matrix[0].size(); c++){ // 状态转移方程： memo[r+1][c+1] = memo[r][c+1] + memo[r+1][c] + matrix[r][c]-memo[r][c]; } } } // 使用memo求出制定区域的元素之和。 int sumRegion(int row1, int col1, int row2, int col2) { return memo[row2+1][col2+1]-memo[row1][col2+1]-memo[row2+1][col1]+memo[row1][col1]; } };

关键：找规律

#70 Climb Staires

• 描述

  1	你爬楼梯，每次只能爬1阶或2阶，那么要爬到n阶，由多少种走法

• 逻辑

  逻辑与斐波那契数列相同。以n=5为例。

  • 状态定义：memo[i]表示爬i阶台阶由多少中爬法。其中定义memo[0]=1, memo[1]=1。

  • 状态转移方程：见下图：

    

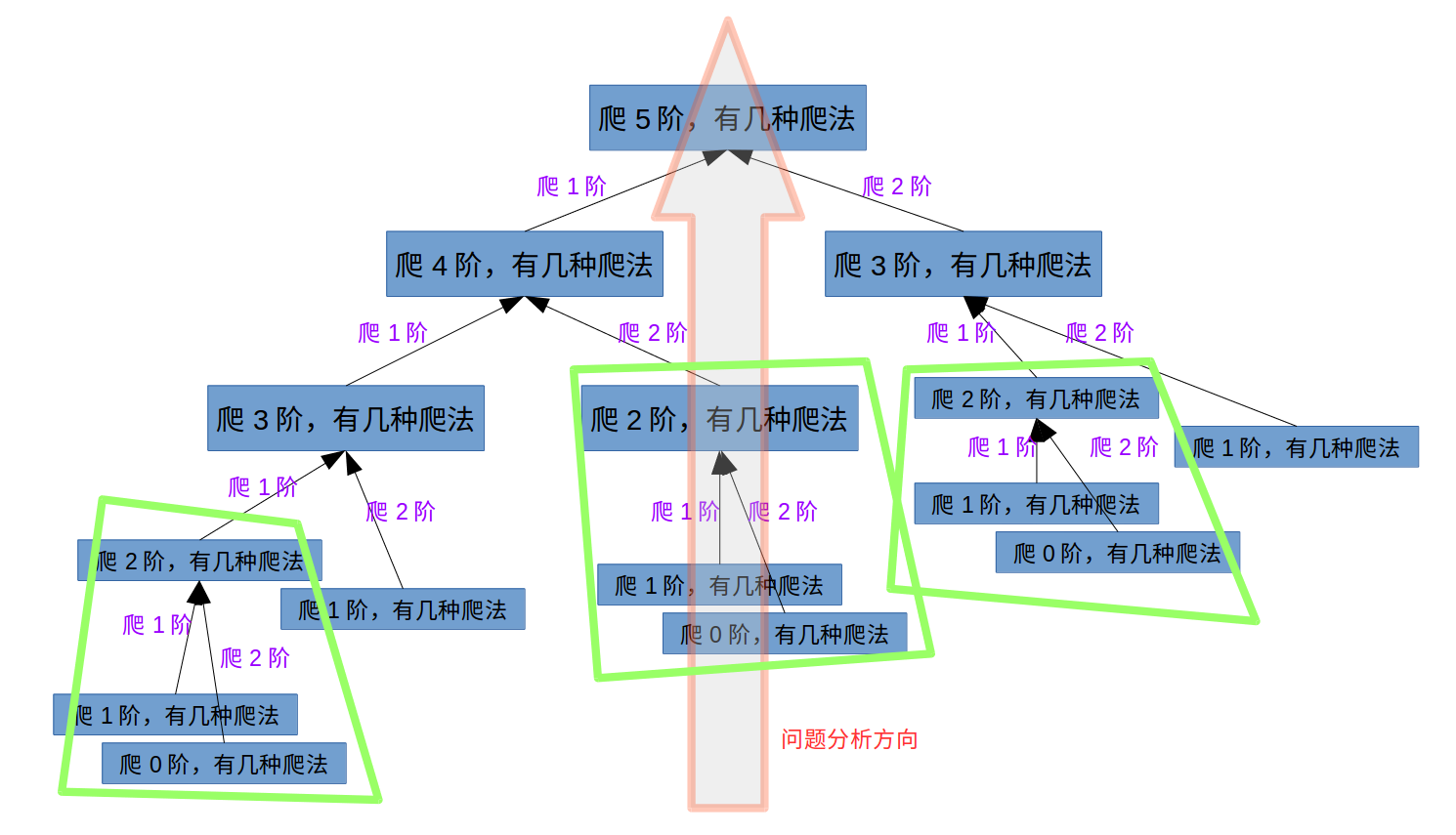
    DP的特点是从已知计算求下一步结果，进而再求下下步结果。计算是由一个特定方向的。所以按照图中箭头方向分析：

    爬2阶的爬法 = 爬1阶的爬法(爬了1阶，再爬1阶) + 爬0阶的爬法(爬了0阶，再爬2阶);
    爬3阶的爬法 = 爬2阶的爬法(爬了2阶，再爬1阶) + 爬1阶的爬法(爬了1阶，再爬2阶);
    爬4阶的爬法 = 爬3阶的爬法(爬了3阶，再爬1阶) + 爬2阶的爬法(爬了2阶，再爬2阶);
    ...

    这一类问题有重复计算的子问题。所以DP的记忆化机制保存了中间的结果，从而避免了重复的计算。

• 实现

  1 2 3 4 5 6 7 8 9 10

  int climbStairs (int numStairs) { vector<int> memo(numStairs + 1, -1); memo[0] = 1; memo[1] = 1; for (int i =2; i <= numStairs; i++) { memo[i] = memo[i-1] + memo[i-2]; } return memo[numStairs]; }

454,

#454 4Sum II

• 描述

  1 2 3 4 5 6 7 8 9 10 11 12 13

  Input: A = [ 1, 2] B = [-2,-1] C = [-1, 2] D = [ 0, 2] Output: 2 Explanation: The two tuples are: 1. (0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0 2. (1, 1, 0, 0) -> A[1] + B[1] + C[0] + D[0] = 2 + (-1) + (-1) + 0 = 0

• 逻辑

  第一步：将A和B中元素的可能和作为key放入map1，value为这个和出现的频数。
  第二步：将C和D中元素的可能和作为key放入map2，value为这个和出现的频数。
  第三步：对于map1中的每个元素，在map2中查找这个元素对应的负数，如果找到，则结果中加上(这个元素的频数)×(map2中这个元素负数的频数)  DONE。

• 实现

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  int fourSumCount(vector<int>& A, vector<int>& B, vector<int>& C, vector<int>& D) { // 第一步 unordered_map<int, int> mp1; for (int a:A){ for (int b:B) mp1[a+b]++; } // 第二步 unordered_map<int, int> mp2; for (int c: C){ for (int d: D) mp2[c+d]++; } // 第三步 int res = 0; for (auto & itr : mp1){ if (mp2.find(-(itr.first)) != mp2.end()) res += (itr.second) * (mp2[-(itr.first)]); } return res; }

  敲黑板理清楚逻辑后再实现。

把线性代数(LA)中每个概念理解清楚，并且理清概念间的来龙去脉。
几乎所有的LA内容都是围绕下面这组等价命题展开的:

对于方阵A(n*n)： 
    1.A可逆(A是非奇异阵)
    2.<=> 线性系统 Ax=0 有唯一解，零解
    3.<=> 线性系统 Ax=b 有唯一解
    4.<=> A的最简化行阶梯矩阵 rref(A)=I 是单位矩阵
    5.<=> A可以表示称一系列初等矩阵的乘积
    6.<=> A的列向量线性无关
    7.<=> A的列向量可以生成n维空间
    8.<=> A的列向量是n维空间的基
    9.<=> A的行秩==A的列秩==n
    10.<=> A满秩(r==n)
    11.<=> A的行空间维度==A的列空间维度==n
    12.<=> A的行向量线性无关
    13.<=> A的行列式 det(A)!=0
    14.<=> 0不是A的特征值

因为真实世界通常是多维度的，单个数已经不足以来描述真实世界。线性代数研究的就是一组数，也就是向量。

向量

向量是一组有序的数，表示方向，如物理世界中。又可以表示多维世界。有序说明了(a, b)和(b, a)是两个不同的向量。

向量有其基本的运算：

1.向量加法
2.数量乘法

由这两个基本操作想到了向量空间。

向量空间

空间是一个集合，我们经常说的2D，3D空间，实际上是欧几里得空间。现在知道，欧几里得空间是点集，又是起点为（0,0）的向量集合。此处所讨论的向量空间默认指的是欧几里得向量空间。

向量空间是个集合，其中的元素必须定义两个基本运算：

1.向量加法
2.数量乘法

这两个基本运算又必须满足十条性质。(这是向量空间的定义)

这两个运算十分重要，因为这使得向量成为向量。

之所以把向量默认为欧几里得空间的向量，是因为现实世界中，欧几里得空间是最常见的。

把不是欧几里得空间的其他空间称为“广义线性空间”。比如，所有的2*2的方阵构成一个向量空间，其中定义向两加法为矩阵加法，定义数量乘法为矩阵的数量乘法。可以证明这个空间中的2*2方阵满足十条性质。

有了空间，就有子空间。

子空间

啥是子空间：如果V是一个向量空间，S是V的子集，而且S也是一个向量空间(或者说，S对加法和数量乘法封闭)，那么称S是V的一个子空间。

比如，2维欧几里得空间是一个向量空间V，现在有一条过（0,0）的直线，所有这条直线上的向量构成V的一个子空间S。可以证明S对加法和数量乘法封闭。

而假如现在由一条不过（0,0）的直线，所有在这条直线的向量空间不是V的子空间。可以证明，这个空间对加法和数量乘法不封闭。

补充一点，之所以（0,0）点是个关键，是因为欧几里得空间的向量起点一定要是（0,0）。

上述例子进一步说，S空间是过（0,0）的一条直线。那么任何这条只直线上的非零向量v都可表示空间S中的其他任何向量，也就是说v可以生成S中的所有向量。那么这个非零向量v就是这个子空间中的一组基，子空间的维度为1。

有一点需要注意，如果一个欧几里得空间中每个实数元素组包含n个元素，这个空间维度一定是n吗？错！正如上述，过原点的一条直线是二维欧几里得空间的一个子空间，这个子空间中每个元素含有x，y两个元素，但是这个子空间的维度是1，非2。

那么什么是空间的一组基呢？

空间的基

先看两个命题：

命题1：如果m个向量生成n维空间，则m最小为n。
命题2：如果m个n维向量线性无关，则m最大为n。

由上述两个命题，可以得到空间基的定义：
若一组向量可以生成整个n维空间，且线性无关，则这组向量一定有n个。这样一组向量是n维空间的的一组基。

基的作用是啥：在n维空间中，如果给定一组基，任何一个向量(或点)都可以表示成这组基的线性组合。而且表示方法唯一。

比如2维欧几里得空间中由无数组基，其中最常使用的是标准正交基：(e1，e2)。e1与e2正交，就是垂直，且模为1。

实际上，我们常说的一个向量，如(12,8)，默认是使用二维欧几里得空间的基来表示的，也就是说，(12,8)左边是默认左乘(e1, e2)=((1,0)T,(0,1)T)。这个乘法表示的含义是，在(1,0)T这个方向上移动12个单位，在(0,1)T这个方向上移动8个单位，后得到的点或坐标(12,8)。

同样这个点也可以使用其他的基来表示。如(u,v)=((4,1)T,(2,3)T)。在这个基中，(12,8)用(2,2)来表示，就是说，在方向(4,1)T上移动2个单位，在(2,3)T方向上移动2个单位，就移动到了(12,8)。所以在(u,v)这组基下(2,2)来表示同一个点。

由上述，可以理解：矩阵A的列向量线性无关+矩阵A可以生成n维空间=>A是方阵且A的列向量是n为空间的基。也就是等假命题6，7，8。

只是用标准正交基不行吗，为什么还要由其他基。因为对于特定的问题，把问题放到其他基会更容易解决问题。

知道了什么是空间的基，那什么是空间的维度呢？

空间的维度

空间维度的定义是：一个空间的基中，向量的个数，称为空间的维度。

如二维欧几里得空间的基(e1,e2)这个基中由两个向量，所以dim()=2。

回看空间基的两个命题，什么叫线性无关? 什么又是“生成n维空间”?

线性无关

定义：对于p个n维向量，存在一组k（p个）全为零时才有，v与对应k相乘后相加的结果为0。则称p个v线性无关。

也就是说，任何一个v都是独立存在的，不能由其他向量的线性组合来代替。

反过来，如果一组向量线性相关，那么表示其中有一个向量可以由其他向量线性表示，这个向量对应的k为0。也就是说，被线性表示的向量不能增加系统的信息量，系统有信息冗余。

把上述“v与对应k相乘后相加”称作v的线性组合。

线性组合

就是向量相乘后相加，体现了向量的两种最基本运算：向量相加，数量乘法。

从矩阵的列视角来看，矩阵与向量的乘法也是个线性组合，是矩阵列向量的线性组合。其中的v以列向量的形式构成矩阵，所有的k构成向量。

另一个例子，Guass-Jordan 消元法，结果的每一行，是原来矩阵各行的一个线性组合。注意，消元法的结果描述的是原矩阵列向量的关系。

生成空间

假如有两个线性无关的二维向量(u,v)，在二维欧几里得空间中的任何一个向量都可以表示成u，v的线性组合，则称u，v可以生成整个二维空间。

可以拓展到n维空间。

但是既然u，v可以生成整个二维空间，那么再增加任意一个向量w，这三个向量u，v，w也能生成整个二维空间。只需要w前的系数为0。问题来了，至少需要多少个向量才能生成整个二维空间呢?结论是：对于n维空间，至少需要n个向量才能生成。用反证法，把问题转化齐次线性方程组解的问题。

看待矩阵的4大视角

视角：

空间视角：列向量  (坐标系或空间)
系统视角：线性方程组
函数视角：行向量 （与线性变换相关）
数据视角：记录与特征

线性系统

啥是线性？所有未知数是一次的。

线性系统就是多个一次方程联立。线性系统中存在一个矩阵叫做增广矩阵。对这个矩阵的操作使用Guass-Jordan消元，返回一个阶梯矩阵。使用这个操作来判断这个线性方程组解的结构。解的结构本质上是经过消元后，方程组的个数与未知数个数的关系。

线性系统中，当等号右边全为零时，叫做其次方程组。

许多LA相关问题都可以经由线性系统的视角，证明线性方程组的解，来证明。

比如：方阵的逆与线性相关的关系。如何判断线性相关否，根据定义来：这几个向量的线性组合（等号右边为0）是否只有零解，若只有零解，表示定义中的k全为零，全为零啥意思，就是所有k对应的所有向量线性无关（线性无关的定义）。 如果方阵A可逆，那么Ax=0 <=> A的逆*A = A的逆*0，即I*x=0（0矩阵）,所以x=0。

也就是说，方阵A可逆，则A的列向量线性无关。

线性变换

变换是一个函数，一个线性变换T(x)必须满足两个条件：

T(u+v)=T(u)+T(v)
T(C*u)=C*T(u), C属于1D欧几里得空间

看，又是加法和数量乘法。
一个线性变换对应一个矩阵。而且所有矩阵都对应一个线性变换。

从几何角度理解特征值特征向量时，因为只给出了一个变换，所以首先那需要判断这个变换是否是一个线性变换，若果是，那么就对应一个矩阵。有了矩阵，才能根据定义找到特征值和特征向量。

基与坐标系

行空间

列空间

方阵的秩

标准正交基

方阵的行列式

行列式只是方阵的一个属性，对于非方阵是没有行列式这一说的(暂时)。方阵A的行列式用det(A) 表示。对于二维欧几里得空间，它由无数个基，怎样来区分彼此呢？可以使用基构成的面积的大小来区分。对于3D欧几里得空间，就是体积了。

所以行列式的几何意义就明确了。由于行列式有正负之分的，所以更确切的说，行列式的几何意义是有向面积或有向体积。

行列式其实是用于研究特征值和特征矩阵的。

行列式的计算在大学是着重练习的，但其实计算不是重点。这里由个通用的计算行列式的方法：

进行Guass消元，
过程中不做归一化，
行置换列置换操作，每一次置换操作，符号改变一次没所以要记录置换了多少次，
最终化为上三角矩阵，即对角线以下为0。

堆中行列式的结果，就是对角向上元素累乘。

补充一点，啥是初等矩阵：对单位矩阵进行初等行操作得到的矩阵。

还有一部分内容是关于行列式的代数表达，涉及到余子式，代数余子式，伴随矩阵，Cramer法则等。代数表达在数学上很优美，但是咋实际计算行列式值时，很低效。行列式中重要的是其性质，之后的LA高阶内容都会用到行列式性质。

特征值特征向量

这又是方阵的另外两个属性。是把方阵作为基，从变换的角度看的。这个变换拥有一些特征，这些特征被特征向量特征值描述。

一个向量在基A中的表达是u，在标准正交基E中的表达是v，如果变换满足A*u=lambda*E*v，而E*v=u，给出一个向量，默认都是用E基表达。lambda为标量。

也就是A*u=lambda*u，也就是说，u和v 同方向。lambda称作方阵A的特征值，u为A对于lambda的特征向量。

• 如何求一个方阵的特征值和特征向量？

  对于A*u=lambda*u.

  • 当u为零向量时，不论A是啥，等号都成立，所以u=0是平凡解。也就是说，u=0不是任何方阵的特征向量。不能表达A的特性。

  • 当lambda=0时，不是平凡解。lambda=0，即A*u=0。是齐次线性方程组。上一条说过了，u不能为0向量。也就是说，A*u=0有非零解。
    回忆：[若A可逆，A*u=0只有零解]，现在条件是，u是其非零解，即A不可逆。
    总结：若lambda=0是A的特征值， 那么A不可逆。即不可逆方阵的一个特征值可以是0.

    接着求，A*u=lambda*E*v => A*u - I*lambda*u = 0 => (A-lambda*I)*u=0 我希望这个表达式有非零解。

    若有非零解，则(A-lambda*I) 不可逆，就是说det(A-lambda*I)=0. （看到了把，行列式在此出现）。

    根据det(A-lambda*I)=0可以求出A的若干特征值lambda，进一步，把lambda带入A*u=lambda*u便可以求得这个lambda对应的特征向量组。

理解的重点：

* A的特征向量不可能是0向量，
* 同一个向量在不同的基中的表示同方向或逆方向，
* 特征值特征向量与变换有关。

• 特征值与特征向量的一些性质：

  • 如果u值A对应于lambda的一个特征向量，则k*u也是lambda的一个特征向量。
  • 如果A的一个lambda=0，则A不可逆。
  • 对角矩阵，上三角矩阵，下三角矩阵的特征值，就是主对角线上元素的值。
  • 如果lambda是A是特征值，则lambda^m 是A^m的特值。
  • 如果lambda是A的特征值，则1/lambda是A的逆的特征值。

• 从几何角度理解特征值和特征向量

  几何中，一个变换，比如投影变换：2D中将任意向量投影到向量(2,3)所在的直线。不一定对应一个矩阵。所以要先判断这个变换是一个线性变换。根据线性变换的内容：满足下面两个条件才是线性变换：
  T(u+v)=T(u)+T(v)
T(C*u)=C*T(u), C属于1D欧几里得空间
  显然投影变换满足上述条件，所以可以得到矩阵A。不过我们不求矩阵A，也可以从几何角度的到这个变换的特征值特征向量。

  投影变换的特征值是什么呢？因为从定义看，特征向量经过变换后与变换前同方向。所以秩序在投影变换图中找那些向量满足变换前后同方向。

  显然对于过(0,0)和(2,3)两点的直线l，其上向量俊满足上述条件。对于特征值，英文l上的 向量投影到自身，还是自身，所以lambda=1。

接着记录leetcode问题：
1002, 4, 215, 88, 674, 950

提炼技术：

• 记录字符频数
• 实时更新
• 额外变量
• 逻辑中由插入操作，考虑使用队列

#1002

• 描述

  1 2 3

  找到单词的共有字符： Input: ["bella","label","roller"] Output: ["e","l","l"]

• 思路

  假设输入单词的列表是：[‘bcdc’, ‘dcc’, ‘cddcb’]
  过程如下：

  loop：对于每一个单词记录其中字母出现的频数count，根据这个count，更新count26。
          当所有单词统计过后，count26就包含了最终每个单词共有的字符出现的频数。
  最后一步：将count26中频数大于0的字母放入res数组。

  其中，count26把元素初始化为可能的最大值；而且是个全局变量，对于每个单词都实时更新其值，节省了空间。

  

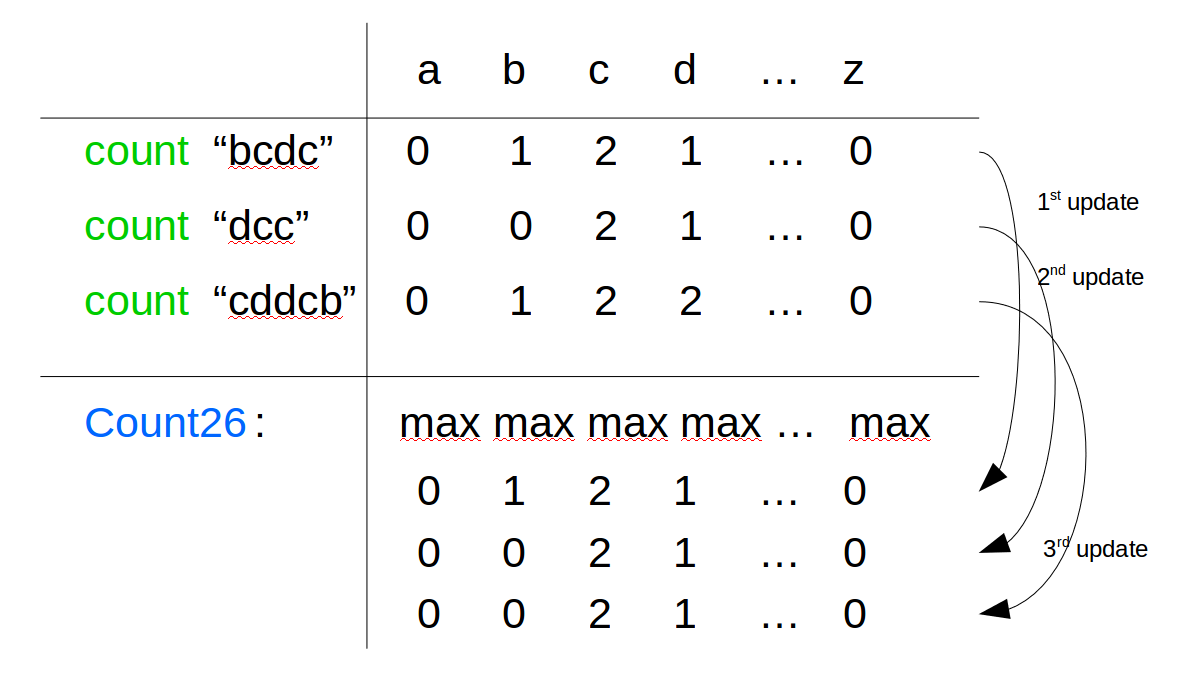
  最终返回两个c一个d：[‘c’,’c’,’d’]。

• 看图说话

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  vector<string> commonChars(vector<string>& A){ vector<int> count26(26, INT_MAX); vector<string> res; for (auto word: A){ // 统计每个单词中每个字母出现的频数 vector<int> count(26, 0); for (auto chara: word){ count[chara - 'a']++; } // 每一个单词统计频数后更新count26 for (int i=0; i<26; i++){ count26[i] = min(count26[i], count[i]); // online update } } // 最终的count26中记录了每个字母出现的次数 for (int i=0; i<26; i++) for (int j=0; j<count26[i]; j++) res.push_back(string(1, i+'a')); // 索引0对应‘a’ return res; }

关键：记录字符频数，实时更新，

#4 Median of Two Sorted Arrays

• 描述

  1 2 3 4 5 6

  There are two sorted arrays nums1 and nums2 of size m and n respectively. Find the median of the two sorted arrays. nums1 = [1, 2] nums2 = [3, 4] The median is (2 + 3)/2 = 2.5

• 思路

  思路直接：第一步：merge两个有序数组，第二步：找到median。

• 实现

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) { int m = nums1.size(); int n = nums2.size(); // aux 数组记录merge后的数组 vector<int> aux(n+m ,0); // merge two sorted arrays int i=0,j=0,k=0; for (k=0; k< m+n; k++){ // 如果i超过了nums1的长度，表示nums1中元素遍历完毕 if (i>=m) aux[k] = nums2[j++]; // 如果j超过了nums2 的长度，表示nums2中元素遍历完毕 else if (j>=n) aux[k] = nums1[i++]; // 如果两个数组都没有遍历完毕 else if(i<m && j<n && nums1[i] < nums2[j] ) aux[k] = nums1[i++]; // 如果两个数组都没有遍历完毕 else if (i<m && j<n && nums1[i] >= nums2[j] ) aux[k] = nums2[j++]; } // 计算中间两个数的median double res = 0; if((m+n)%2 == 0) res = 0.5*(aux[(m+n)/2] + aux[(m+n)/2-1]); else if((m+n)%2 == 1) res = (aux[(m+n)/2]); return res; }

  其实在后两个if else语句中的i<m && j<n是多余的，因为，如果执行到了这里，i<m && j<n就已经满足了。

关键：merge操作的情况要考虑清楚，所有情况要完备且neat，功能实现无误后，将冗余的删除。

#215 Kth largest element

• 描述

  1 2	Input: [3,2,1,5,6,4] and k = 2 Output: 5

• 逻辑

  1. 当数组中的元素可以是任何整数时：

     先排序，后直接取第k个元素（no good）

  2. 当数组中的元素中只含有0~9这10个，可以有其他方法：

     使用频数数组记录每个digit出现的次数，根据这个频数与k的关系取到最终值。

  3. 一般的方法：

     Top-k 问题，使用冒泡排序，秩序要冒泡k次。

• 实现

  1. 第一种情况：

     1 2 3 4 5 6 7 8 9 10

     struct Increase{ bool operator()(const int& a, const int& b){ return a>b; } }; int findKthLargestElement(vector<int>& nums, int k){ sort(nums.begin(), nums.end(), Increase()); return nums[k-1]; }

  2. 第二种情况可以使用如下方式：

     1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

     int findKthLargestElement(vector<int>& nums, int k){ int res = 1; // 与k比较 int count[10] = {0}; // 频数记录 for (int i=0; i<nums.size(); i++){ count[nums[i]]++; } for (int i=9; i>=0; i--){ if (count[i] == 0) continue; for (int j=1; j<=count[i]; j++){ if (res < k) res+=1; else if(res == k) return i; } } throw invalid_argument("no return"); }

#88 Merge Two Array

• 描述

  1 2 3 4 5 6 7

  Input: nums1 = [1,2,3,0,0,0], m = 3 nums2 = [2,5,6], n = 3 Output: [1,2,2,3,5,6] NOTE: num1&num2 are sorted

• 逻辑

  其实就是实现Merge Sort的一个树结点的操作

• 实现

  1 2 3 4 5 6 7 8 9 10 11 12 13 14

  vector<int> merge2(vector<int>& nums1, int m, vector<int>& nums2, int n) { int i=0; //def num1 的index int j=0; //def num2 的index int k=0; //def 结果array的index vector<int> arr(m+n); while(i<m || j<n){ if(nums1[i] <= nums2[j]) arr[k++] = nums1[i++]; else arr[k++] = nums2[j++]; } return arr; }

#674 最长连续递增子序列的长度

• 描述

  1 2 3

  比如：nums=[1,3,7,5,6,8,9] 返回4. 最长递增子序列是[5,6,8,9]

• 逻辑

  用变量start标记每个递增子序列的第一个数的索引。
  遍历nums数组，只要nums[i]<=nums[i-1]，更新start为当前索引i。
  i每次加1，res更新一次：res=max(res, i-start+1).

• 实现

  1 2 3 4 5 6 7 8 9 10

  int func(vector<int>& nums){ int res = 0; int start = 0; // extra variable for (int i=0;i<nums.size();i++){ if(i>0 && nums[i]<=nums[i-1]) start=i; res = max(res, i-start+1); // update } return res; }

  关键： 额外变量，实时更新，先手动实现，

#950 Reveal Cards In Increasing Order

• 描述

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  给出一个序列，含若干个元素，任意顺序，现在确定一种顺序S，使得这个顺序的序列执行如下操作的过程中，第一步取出元素为递增顺序。这个操作如下： 1. 取出序列的第一个元素 2. 如果此时序列中还有元素，将第一个元素放到序列尾部。 3. 只要序列中有元素，就执行1,2步骤。 返回S。 例： Input: [17,13,11,2,3,5,7] Output: [2,13,3,11,5,17,7] Explanation: We get the deck in the order [17,13,11,2,3,5,7] (this order doesn't matter), and reorder it. After reordering, the deck starts as [2,13,3,11,5,17,7], where 2 is the top of the deck. We reveal 2, and move 13 to the bottom. The deck is now [3,11,5,17,7,13]. We reveal 3, and move 11 to the bottom. The deck is now [5,17,7,13,11]. We reveal 5, and move 17 to the bottom. The deck is now [7,13,11,17]. We reveal 7, and move 13 to the bottom. The deck is now [11,17,13]. We reveal 11, and move 17 to the bottom. The deck is now [13,17]. We reveal 13, and move 17 to the bottom. The deck is now [17]. We reveal 17. Since all the cards revealed are in increasing order, the answer is correct.

• 逻辑

  1. 既然初始序列deck是任意的，所以先排序，从大到小排序得到新deck。

  2. 过程中需要插入序列第二个位置，所以考虑使用双端队列为容器dq。把第一个元素放入队列，从第二个元素开始。

     • 第一步 将队列的最后元素插入队列的第一个位置。
     • 第二步 将当前序列中的元素deck[i] 插入队列首。
     • 第三步 将此时的队列中最后元素删除。

• 实现

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

  vector<int> deckRevealedIncreasing(vector<int>& deck){ sort(deck.begin(), deck.end(), [](int& a, int& b)->bool{ return a>b; }); deque<int> dq; dq.push_front(deck[0]); for (int i=1; i< deck.size(); i++){ dq.insert(dq.begin(), *(dq.end()-1)); dq.push_front(deck[i]); dq.pop_back(); } return vector<int>(dq.begin(), dq.end()); }

关键： 已知结果求原因，反推过去，
逻辑中由插入操作，考虑使用队列、
双端队列常用方法： push_front(), push_back(), pop_back(), pop_front(), insert()

接着记录数组相关问题。
56, 74, 240, 136, 1122, 1009, 868, 985,

常用技术：

• 粗调+精调
• XOR性质
• 额外变量的使用
• 数进制间的对应(相互为等价信息)
• 移位操作
• 首先想到的方法不是好的方法

#56 Merge intervals 合并区间

• 描述

  1 2 3

  Input: [[1,3],[2,6],[8,10],[15,18]] Output: [[1,6],[8,10],[15,18]] Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].

• 思路

  第一步：按区间左边界排序
  第二步：把第一个interval[0]放入结果容器res中，从第二个interval[1]开始：
      如果interval[1]的左边界 >= res的最后一个interval的右边界，表示两者无交集，
          把interval[1] append到res中；
      如果interval[1]的左边界 < res的最后一个interval的右边界，表示两者有交集，
          把interval[1]的右边界写入res最后一个interval的右边界。

  第二步过程间下示意图：

  

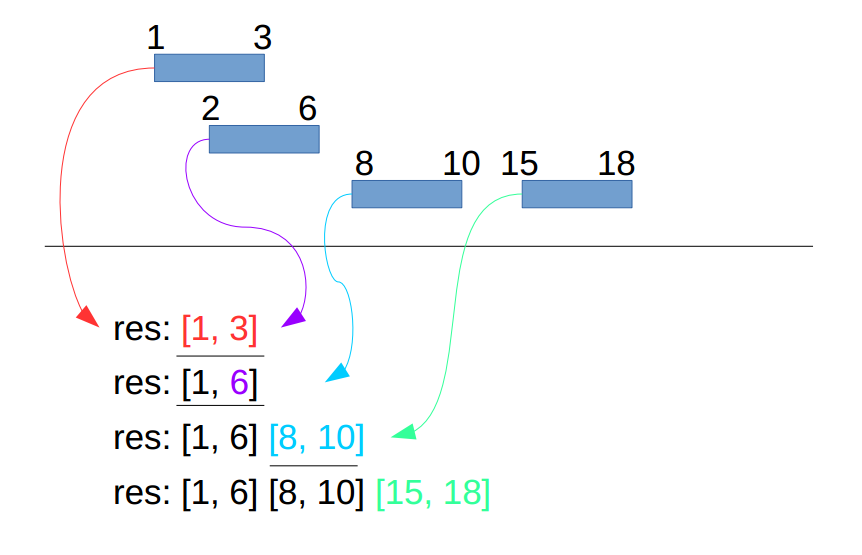
• 看图说话实现

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  static bool compare(vector<int>& a , vector<int>& b){ return a[0] < b[0]; } vector<vector<int>> merge(vector<vector<int>>& intervals) { vector<vector<int>> res; if (intervals.size()==0) return res; if (intervals.size()==1){ res.push_back(intervals[0]); return res; } // 区间左端点从小到大排序 sort(intervals.begin(), intervals.end(), compare); res.push_back(intervals[0]); int i=1; while(i < intervals.size()){ vector<int>& last = res.back(); // 注意 if (last[1] < intervals[i][0]){ res.push_back(intervals[i]); }else{ last[1] = max(last[1], intervals[i][1]); } i++; } return res; }

关键： vector<int>& last = res.back(); 定义last 的类型是reference。由逻辑，凡是last被修改，就是res.back()被修改，所以last和res.back()为一个对象。

#64 Search 2D matrix

• 描述

  1 2 3 4 5 6 7 8 9 10 11

  Input: matrix = [ [1, 3, 5, 7], [10, 11, 16, 20], [23, 30, 34, 50] ] target = 16 Output: true 1.Integers in each row are sorted from left to right. 2.The first integer of each row is greater than the last integer of the previous row.

• 思路

  根据问题的特点，设计粗调+精调方法：

  粗调：把每一行的最后一个元素放入新的数组中（m长度）: [7, 20, 50].
      用target与其中的每个元素比较，找到第一个比target大的元素并返回index。
      如：20 是第一个大于target的元素，返回1，即target在index=1的行。
  精调：在index=1的行中搜索target。

• 实现

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  bool searchMatrix(vector<vector<int>>& matrix, int target){ int row = matrix.size(); int col = matrix[0].size(); vector<int> station(row, 0); for (int r=0; r<row; r++) station[r] = matrix[r][col-1]; // rough-tuning int pr = 0; for (int i=0; i<station.size(); i++){ if (target == station[i]) return true; if (target < station[i]){ pr = i; break; } } // fine-tuning for (int c=0; c<col; c++){ if (matrix[pr][c] == target) return true; } return false; }

• 关键： 粗调&精调

#240 Search 2D matrix II

• 描述

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  Consider the following matrix: [ [1, 4, 7, 11, 15], [2, 5, 8, 12, 19], [3, 6, 9, 16, 22], [10, 13, 14, 17, 24], [18, 21, 23, 26, 30] ] Given target = 5, return true. Given target = 20, return false. 1.Integers in each row are sorted in ascending from left to right. 2.Integers in each column are sorted in ascending from top to bottom.

• 思路

  与#74不同，对于方阵，可以使用粗调精调，但是对于非方阵，此法复杂。考虑新的方法，如下图：

  

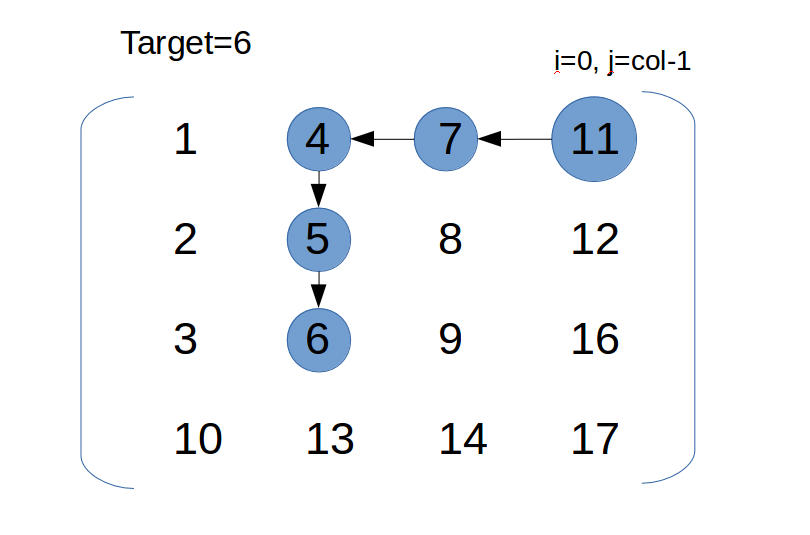
  从右上角或(左下角开始)，target与所到元素比较：

  if (target > matrix[i][j]) i++;    // 向下走
  else if (target < matrix[i][j]) j--;    // 向右走
  else if（target == matrix[i][j]）return true  // 找到

• 看图说话

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  bool searchMatrix(vector<vector<int>>& matrix, int target) { int row = matrix.size(); if (row == 0) return false; int col = matrix[0].size(); if (col == 0) return false; if (target < matrix[0][0] || target > matrix[row-1][col-1]) return false; int r = row-1; int c = 0; while(r >= 0 && c < col ){ if (target == matrix[r][c]) return true; else if (target > matrix[r][c]) c++; else r--; } return false; }

#136 Single Number

• 描述

  1 2 3 4 5

  Given a non-empty array of integers, every element appears twice except for one. Find that single one. Input: [4,1,2,1,2] Output: 4

• 思路

  方法一： map
  方法二： set
  方法三： XOR 使用XOR的数学性质，可以很快地解决问题

  XOR 数学性质
      I)   a^0=a (a!=0)
      II)  a^a=0 (a!=0)
      III) a^b^a = a^a^b = b^a^a = b 

• 实现

  1 2 3 4 5 6 7

  int singleNumber(vector<int>& nums){ int res = 0; for (auto i: nums) res ^= i; return res; }

关键: XOR行为

#1122 Relative Sort Array

• 描述

  1 2 3 4 5 6 7 8 9

  Given two arrays arr1 and arr2, the elements of arr2 are distinct, and all elements in arr2 are also in arr1. Sort the elements of arr1 such that the relative ordering of items in arr1 are the same as in arr2. Elements that don't appear in arr2 should be placed at the end of arr1 in ascending order. Input: arr1 = [2,3,1,3,2,4,6,7,9,2,19], arr2 = [2,1,4,3,9,6] Output: [2,2,2,1,4,3,3,9,6,7,19]

• 思路

  很直接，遍历arr2，对于arr2中所有元素，在arr1中找到这个元素，并且放到合适的位置，这个位置由变量index指示。看下图：

  

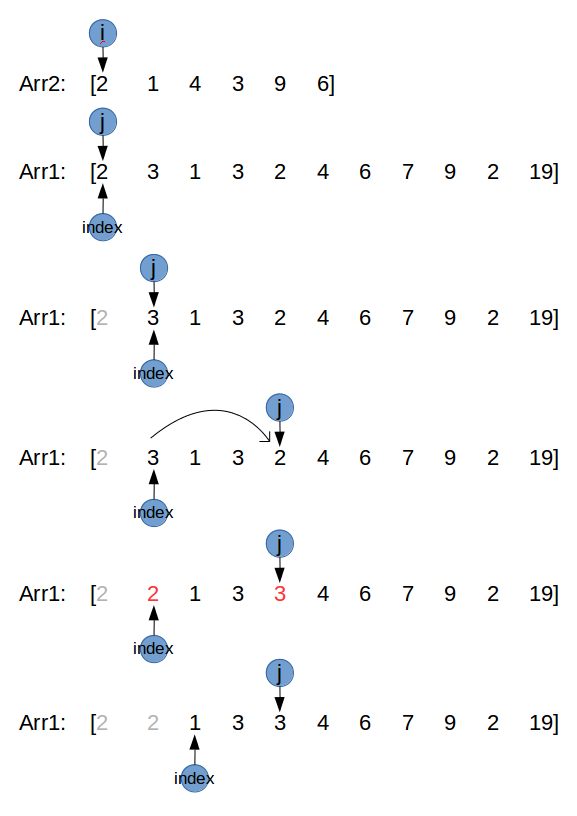
• 看图说话

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  vector<int> relativeSortArray(vector<int>& arr1, vector<int>& arr2){ int index = 0; // extra variable for (int i=0; i<arr2.size(); i++){ for (int j=index; j<arr1.size(); j++){ if (arr1[j]==arr2[i]){ swap(arr1[j], arr1[index]); index++; } } } sort(arr1.begin()+index, arr1.end()); return arr1; }

关键： 额外变量的使用

#1009 Complement of Base 10 Integer

• 描述

  1 2 3

  Input: 10 Output: 5 Explanation: 10 is "1010" in binary, with complement "0101" in binary, which is 5 in base-10.

• 思路

  找到对应的111…1，减去已知，得结果。
  假设N=5，规律：

  binary	dec	公式	判断
  1	1	0*2+1	5>1
  11	3	1*2+1	5>3
  111	7	3*2+1	5<7 =>7-5=2
  1111	15	7*1+1
  11111	31	15*2+1

• 看图说话

  1 2 3 4 5 6

  int bitwiseComplement(int N){ int x = 1; while (N>x) x = x*2+1; return x-N; }

关键：找到规律，数进制间的对应，

#868 Binay Gap

• 描述

  1 2 3 4 5 6 7

  Input: 22 Output: 2 Explanation: 22 in binary is 0b10110. 1 <= N <= 10^9 其中相邻1与1之间距离最大的是2，所以返回2.

• 思路

  规律：一个整数的奇偶与其二进制的尾数相关，奇数对应位二进制的尾数是1；偶数对应二进制的尾数是0. 假如N=22：

  N	左移一位结果	结果的二进制	与N的关系
  22		10110	N左移0位
  22>>1	11	01011	N左移1位
  11>>1	5	00101	N左移2位
  5>>1	2	00010	N左移3位
  2>>1	1	00001	N左移4位
  1>>1	0	00000	N左移5位

• 两方法实现

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

  ///time: O(logN) /// space: O(logN) int binaryGap(int N){ vector<int> index; int k=0; int yu; while (N!=0){ k++; yu = N%2; if (yu == 1) index.push_back(k); N/=2; } int res=0; for (int i=0; i<index.size()-1; i++){ res = max(res, index[i+1]-index[i]); } return res; } ///time: O(logN) /// space: O(1) int binaryGap(int N){ int last = -1, res=0; for (int i=0; i<32; i++){ if (((N>>i)&1) > 0) { if (last >= 0) res = max(res, i-last); last = i; } } return res; }

关键：移位操作，找到问题的等价信息

#985 Sum of Even Numbers After Queries

• 描述

  1 2 3 4 5 6 7 8

  Input: A = [1,2,3,4], queries = [[1,0],[-3,1],[-4,0],[2,3]] Output: [8,6,2,4] Explanation: At the beginning, the array is [1,2,3,4]. After adding 1 to A[0], the array is [2,2,3,4], and the sum of even values is 2 + 2 + 4 = 8. After adding -3 to A[1], the array is [2,-1,3,4], and the sum of even values is 2 + 4 = 6. After adding -4 to A[0], the array is [-2,-1,3,4], and the sum of even values is -2 + 4 = 2. After adding 2 to A[3], the array is [-2,-1,3,6], and the sum of even values is -2 + 6 = 4.

• 思路

  第一步：原始A数组偶数求和sum

  第二步：对于queries中的每个元素执行如下操作：

  1. 如果A中待改变索引的数为even，则从sum中把这个索引对应的数减去。(因为不知道更新后的实际是偶)
  2. 更新A数组。
  3. 更新后的A中被修改的数如果是even，则把他加到sum中。(更新后的奇偶知道了)
  4. 记录sum。

• 实现

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  vector<int> sumEvenAfterQueries(vector<int>& A, vector<vector<int>>& queries) { vector<int> res; int sum = accumulate(A.begin(), A.end(), 0, [](int s, int a){ return s+(a%2==0?a:0); }); for (auto q:queries){ if(A[q[1]]%2==0) sum-=A[q[1]]; // 1. A[q[1]] += q[0]; //2. if (A[q[1]]%2==0) sum+=A[q[1]]; //3. res.push_back(sum); // 4. } return res; }

关键：直接想到的方法通常不是最好的，lambda函数

将这些操作变为肌肉记忆。
可以将常用操作写进配置文件文件中。

1. vim 对应的配置文件 ~.vimrc
2. neovim 对应的配置文件 ~.config/nvim/init.vim

• Open files

  vi a.txt b.txt -O   :窗口打开两个文件

• Command Mode

  :           :进入Command Mode
  e!          :重新加载文件，撤销这次修改
  set nu      :加上行号   .vimrc
  syntax on   :语法高亮   .vimrc
  help s      :查看s的文档
  ls          :列出打开的文件（所有的buffer）
  b a.txt     :跳到a.txt
  e b.txt     :打开b.txt 加入另一个buffer
  vs          :当前文件分一个窗口显示
  vs a.txt    :分窗口打开a.txt
  ZZ          :关闭这个窗口，但不退出对应的buffer
  
  ctrl w w            :光标移动到下一个文件
  
  ctrl w =            :所有窗口等宽度
  ctrl w |            :最大化当前窗口
  ctrl w p            :回到上一个窗口

• Insert Mode

  ctrl u  :删除当前行 从行首到当前位置的内容
  ctrl h  :删除当前位置前一个字符
  ctrl w  :删除当前单词 从单词首到当前位置内容

• Visual Mode

  Visual Mode的一般操作步骤：进入Visual Mode，后选择所需内容，对所选内容进行操作。

  v   :从Normal Mode进入Visual Mode
  V   :从Normal Mode进入Visual Mode 并且选中当前行

• Visual block mode

  ctrl v  :进入visual block 模式 
  
  多行注释：
          1. 进入visual block Mode，选中所需要猪似的所有行
          2. 按大写i，在输出注释符//，按esc，全行注释
  取消多行注释：
          1. 进入visual block Mode，选中所需要删除的行和列
          2. 按d删除

• Normal Mode (即Read Mode，是进入Vim的默认模式，Esc返回Normal Mode)

  a   :从当前位置的下一个位置 进入Insert Mode
  i   :从当前位置开始 进入Insert Mode
  
  I   :从当前行行首开始 进入Insert Mode
  A   :从当前行行尾开始 进入Insert Mode
  
  o   :从下一行的行首 进入Insert Mode
  O   :从上一行的行首 进入Insert Mode
  
  gg      :跳到整个文件的首行
  25gg    :跳到25行行首
  G       :跳到整个文件的尾行
  
  H/M/L   :移动到窗口的高/中/低位置
  
  ctrl u  :向上翻页
  ctrl f  :向下翻页
  
  zz  :当前行放到窗口的中间
  
  w/b      :以单词为单位移动 向后移动/向前移动
  h/j/k/l  :以字符为单位移动 左/下/上/右
  
  0   :移到行首
  $   :移到行尾
  
  y   :复制
  yiw :复制这个词
  yy  :复制这一行
  p   :粘贴到下一行
  P   :大p粘到上一行
  dd  :删除这一行
  diw :删除这个词
  
  u   :撤销这一步
  ZZ  :保存并退出
  
  ctrl s/ctrl q   :锁vim窗口/解锁窗口

• Combo operations

  ciw     :进入insert mode 更改这个单词 i表示“in”
  viw     :选中这个单词
  caw     :改变这个单词
  viw->y->viw->p  :拷贝一个单词从这里拷贝到那里        
  
  vi(     :选中括号中内容
  ci"     :改变这一行中“”中内容 
  ci[     :改变这一行中[]中内容
  vi"     :选中这一行中“”中内容
  yi)     :选择()中所有内容
  da[     :删除[]中所有内容
  
  dt"     :删除从此到“的内容 t表示“to”
  di<
  :% s/XXX/YYY/g     :用YYY替换XXX   
  :32,65d            :delete from line 32 to line 65,  
  
  v, $, y :从此处复制到行尾
  v, $, p :从此处粘贴到行尾 
  
  ggvG    :全选

• 从外部拷贝内容进vim，3步走：

  :set paste
  粘贴操作
  :set nopaste  //自动缩进才会起作用

• 命令中的字母含义

  gg,G        : top, bottom
  d,c,y,v     : delete, change, copy, visually select
  w,s,p,t     : words, sentences, paragraphs, tags(HTML)
  a,i,t,f,F   : all, in, till, find formard, find Backward

• Code 补全

  ctrl n + ctrl p     :自动补全词

• 查询且高亮

  :set incsearch  :一边查一边高亮     
  :set hlsearch   :查询结果高亮      
  /JUNHUI         :(normal mode下)查询字符“JUNHUI”，n定位到下一个，N定位到上一个。 

• 有用插件

  • NERDTree:显示目录的插件。

    使用方法：cd到project目录->进入nvim->Command Mode输入:NERDTree，即可显示当前project的文件和文件夹。

    可以使用<Leader>快捷键避免繁复输入NERDTree。类似的设置要写入配置文件。